题目内容
 如图,函数y=
如图,函数y=| k |
| x |
(1)求k的值及B点的坐标;
(2)若线段AC=2,求线段AB的长.
考点:反比例函数系数k的几何意义,反比例函数图象上点的坐标特征
专题:
分析:(1)根据反比例函数k的几何意义得到S△AOC=
|k|=2,可解得k=4,则反比例函数解析式为y=
,然后利用反比例函数图象上点的坐标特征确定B点坐标;
(2)由AC=2,S△AOC=2可得OC=2,则A点坐标为(2,2),然后根据两点间的距离公式可计算出线段AB的长.
| 1 |
| 2 |
| 4 |
| x |
(2)由AC=2,S△AOC=2可得OC=2,则A点坐标为(2,2),然后根据两点间的距离公式可计算出线段AB的长.
解答:解:(1)∵AC⊥x轴于C
∴S△AOC=
|k|=2,
而k>0,
∴k=4,
∴反比例函数解析式为y=
,
把B(1,m)代入得m=4,
∴B点坐标为(1,4);
(2)∵AC=2,
而S△AOC=2,
∴OC=2,
∴A点坐标为(2,2),
∴AB=
=
.
∴S△AOC=
| 1 |
| 2 |
而k>0,
∴k=4,
∴反比例函数解析式为y=
| 4 |
| x |
把B(1,m)代入得m=4,
∴B点坐标为(1,4);
(2)∵AC=2,
而S△AOC=2,
∴OC=2,
∴A点坐标为(2,2),
∴AB=
| (2-1)2+(2-4)2 |
| 5 |
点评:本题考查了反比例函数比例系数k的几何意义:在反比例函数y=
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了反比例函数图象上点的坐标特征和两点间的距离公式.
| k |
| x |

练习册系列答案
相关题目
下列说法不正确的是( )
| A、有一个角是直角的平行四边形是正方形 |
| B、对角线相等的菱形是正方形 |
| C、对角线互相垂直的矩形是正方形 |
| D、一组邻边相等的矩形是正方形 |
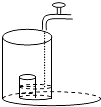 将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )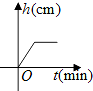
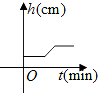
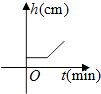
 如图,已知AD=DB=BC,∠C=22°,那么∠ADE=
如图,已知AD=DB=BC,∠C=22°,那么∠ADE=