题目内容
甲乙两人在一环形场地上锻炼,甲骑自行车,乙跑步,甲比乙每分钟快200m,两人同时从起点同向出发,经过3min两人首次相遇,此时乙还需跑150m才能跑完第一圈.
(1)求甲、乙两人的速度分别是每分钟多少米?(列方程或者方程组解答)
(2)若两人相遇后,甲立即以每分钟300m的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过1.2min两人再次相遇,则乙的速度至少要提高每分钟多少米?
(1)求甲、乙两人的速度分别是每分钟多少米?(列方程或者方程组解答)
(2)若两人相遇后,甲立即以每分钟300m的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过1.2min两人再次相遇,则乙的速度至少要提高每分钟多少米?
考点:一元一次方程的应用
专题:
分析:(1)可设乙的速度是每分钟x米,则甲的速度是每分钟(x+200)米,两人同向而行相遇属于追及问题,等量关系为:甲路程与乙路程的差=环形场地的路程,列出方程即可求解;
(2)在环形跑道上两人背向而行属于相遇问题,等量关系为:甲路程+乙路程=环形场地的路程,列出算式求解即可.
(2)在环形跑道上两人背向而行属于相遇问题,等量关系为:甲路程+乙路程=环形场地的路程,列出算式求解即可.
解答:解:(1)设乙的速度是每分钟x米,则甲的速度是每分钟(x+200)米,依题意有
3x+150=200×3,
解得x=150,
x+200=150+200=350.
答:甲的速度是每分钟350米,乙的速度是每分钟150米.
(2)(200×3-300×1.2)÷1.2
=(600-360)÷1.2
=240÷1.2
=200(米),
200-150=50(米).
答:乙的速度至少要提高每分钟50米.
3x+150=200×3,
解得x=150,
x+200=150+200=350.
答:甲的速度是每分钟350米,乙的速度是每分钟150米.
(2)(200×3-300×1.2)÷1.2
=(600-360)÷1.2
=240÷1.2
=200(米),
200-150=50(米).
答:乙的速度至少要提高每分钟50米.
点评:本题考查环形跑道上的相遇问题和追及问题.相遇问题常用的等量关系为:甲路程+乙路程=环形跑道的长度,追及问题常用的等量关系为:甲路程-乙路程=环形跑道的长度.

练习册系列答案
相关题目
 图中几何体的左视图是( )
图中几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
下列说法正确的是( )
| A、无限小数都是无理数 |
| B、无理数都是无限小数 |
| C、有理数只是有限小数 |
| D、实数可以分为正实数和负实数 |
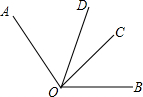 如图,已知:OD是∠AOB的平分线,∠AOC=2∠COB.
如图,已知:OD是∠AOB的平分线,∠AOC=2∠COB. 如图,函数y=
如图,函数y= 如图所示,已知直线AB,CD相交于点O,OF平分∠BOC,∠DOE=90°,∠AOE=44°18°,求∠BOF和∠BOE的大小.
如图所示,已知直线AB,CD相交于点O,OF平分∠BOC,∠DOE=90°,∠AOE=44°18°,求∠BOF和∠BOE的大小.