题目内容
 如图,已知AD=DB=BC,∠C=22°,那么∠ADE=
如图,已知AD=DB=BC,∠C=22°,那么∠ADE=考点:等腰三角形的性质
专题:
分析:根据等边对等角的性质可得∠BDC=∠C,∠ABD=∠A,再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠ABD,∠ADE的度数.
解答:解:如图,∵AD=DB=BC,
∴∠BDC=∠C,∠ABD=∠A,
在△BCD中,∠ABD=∠BDC+∠C=22°+22°=44°,
∴∠A=44°,
在△ACD中,∠ADE=∠A+∠C=44°+22°=66°.
故答案为:66.
∴∠BDC=∠C,∠ABD=∠A,
在△BCD中,∠ABD=∠BDC+∠C=22°+22°=44°,
∴∠A=44°,
在△ACD中,∠ADE=∠A+∠C=44°+22°=66°.
故答案为:66.
点评:本题主要考查了等腰三角形的性质,三角形的外角性质,主要利用了等边对等角,三角形的一个外角等于与它不相邻的两个内角的和的性质.

练习册系列答案
相关题目
 如图,△ABC与△A1B1C1关于直线l对称,则∠B的度数为( )
如图,△ABC与△A1B1C1关于直线l对称,则∠B的度数为( )| A、50° | B、30° |
| C、100° | D、90° |
用同样大小的黑色棋子按如图所示的规律摆放,则第100个图中有棋子( )


| A、300枚 | B、301枚 |
| C、303枚 | D、304枚 |
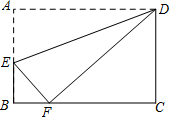 如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处.若∠CDF=50°,则∠ADE为
如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处.若∠CDF=50°,则∠ADE为 如图,函数y=
如图,函数y=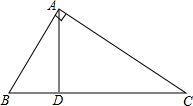 如图,在Rt△ABC中,∠CAB=90°,AD⊥BC,若AB=6,AC=8.
如图,在Rt△ABC中,∠CAB=90°,AD⊥BC,若AB=6,AC=8. 一块三角形的材料被折断了一个角,余下的形状如图,请根据所剩的材料如何推算处所缺角的度数.(写出必要的文字说明及画出相应的图形)
一块三角形的材料被折断了一个角,余下的形状如图,请根据所剩的材料如何推算处所缺角的度数.(写出必要的文字说明及画出相应的图形)