题目内容
10．抛物线y=x2-x-2与x轴的两个交点之间的距离的是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 首先根据题意可得到方程x2-x-2=0，然后再解方程得到x的值，进而得到交点坐标，从而得到答案．
解答 解：∵抛物线y=x2-x-2与x轴有两个交点，
∴x2-x-2=0，
解得：x1=2，x2=-1
∴两个交点坐标是；（2，0）（-1，0），
∴两个交点之间的距离是3，
故选C．
点评 此题主要考查了抛物线与x轴的交点，关键是掌握求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y=0，即ax2+bx+c=0，解关于x的一元二次方程即可求得交点横坐标．
练习册系列答案
互动英语系列答案
相关题目
如图，△ABC的顶点坐标分别为A（4，5），B（2，3），C（5，1）．
15．甲、乙两名队员参加射击训练，成绩分布被制成下列两个统计图：
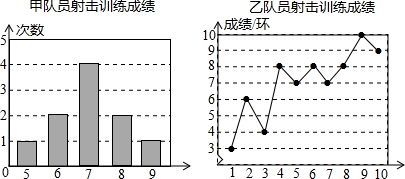
根据以上信息，整理分析数据如下：
（1）写出表格中a，b，c的值；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？
根据以上信息，整理分析数据如下：
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | 7 | b | 7 | c |
| 乙 | a | 7.5 | 8 | 4.2 |
（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？
2．
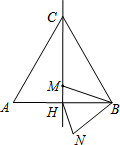如图，边长为4a的等边三角形ABC中，M是高CH所在直线上的一个动点，连结MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN长度的最小值是（ ）
如图，边长为4a的等边三角形ABC中，M是高CH所在直线上的一个动点，连结MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN长度的最小值是（ ）| A． | 2a | B． | a | C． | $\frac{1}{2}$a | D． | $\frac{1}{3}$a |