题目内容
3.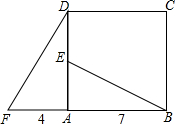 如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7,
如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7,(1)求DE的长度;
(2)探索:BE与DF的位置关系.
分析 (1)根据旋转的性质可得△AFD≌△AEB,再根据全等三角形的性质可得AE=AF=4,根据DE=AD-AE代入数据计算即可得解;
(2)延长BE与DF相交于点G,然后求出∠GDE+∠DEG=90°,再根据垂直的定义解答.
解答  解:(1)根据旋转的性质可知:△AFD≌△AEB,
解:(1)根据旋转的性质可知:△AFD≌△AEB,
所以,AE=AF=4,
∵AB=7,
∴AD=AB=7,
∴DE=AD-AE=7-4=3;
(2)BE与DF是垂直关系.
延长BE与DF相交于点G,
∵∠EAF=90°,∠EBA=∠FDA,
∴∠GDE+∠DEG=90°,
∴BE⊥DF,
即BE与DF是垂直关系.
点评 本题考查了旋转的性质,正方形的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
11.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
 已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求∠BAD的度数与AD的长.
已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求∠BAD的度数与AD的长.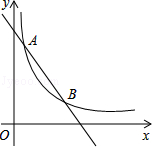 如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.