题目内容
2.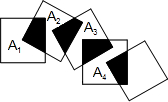 将五个边长都为2的正方形按如图所示摆放,点A1、A2、A3、A4分别是四个正方形的中心,则图中四块阴影部分的面积的和为4.
将五个边长都为2的正方形按如图所示摆放,点A1、A2、A3、A4分别是四个正方形的中心,则图中四块阴影部分的面积的和为4.
分析 作A1E⊥A2E,A1F⊥A2H,由正方形的性质易证△A1HF≌△A1GE,进而可得四边形A2HA1G的面积=四边形A1EA2F的面积=$\frac{1}{4}$×4=1,问题得解.
解答 解:作A1E⊥A2E,A1F⊥A2H.
则∠FA1E=∠HA1G=90°,
∴∠FA1H=∠GA1E,
在△A1HF和△A1GE中,
$\left\{\begin{array}{l}{∠F{A}_{1}H=∠G{A}_{1}E}\\{{A}_{1}F={A}_{1}E}\\{∠{A}_{1}FH=∠{A}_{1}EG}\end{array}\right.$,
∴△A1HF≌△A1GE,
∴四边形A2HA1G的面积=四边形A1EA2F的面积=$\frac{1}{4}$×4=1,
同理,各个重合部分的面积都是1.
则5个这样的正方形重叠部分(阴影部分)的面积和为1×(5-1)=5-1=4,
故答案为:4.
点评 本题主要考查了正方形的特性及面积公式,解答本题的关键是发现每个阴影部分的面积都等于正方形面积的$\frac{1}{4}$.

练习册系列答案
相关题目
10.已知线段AB=8cm,点C是直线AB上一点,BC=2cm,若M是AB的中点,N是BC的中点,则线段MN的长度为
( )
( )
| A. | 5cm | B. | 5cm或3cm | C. | 7cm或3cm | D. | 7cm |
17.汽车向南行驶10千米记作10千米,那么汽车向北行驶10千米记作( )
| A. | 0千米 | B. | -10千米 | C. | -20千米 | D. | 10千米 |
14.矩形具有而一般平行四边形不具有的特征是( )
| A. | 对边相等 | B. | 对角相等 | C. | 对角线相等 | D. | 对角线互相平分 |
11.已知点P(2-a,3a+6)到两坐标轴的距离相等,则点P的坐标为( )
| A. | (3,3)或(6,-6) | B. | (3,-3)或 (6,-6) | C. | (3,3) | D. | (3,-3) |
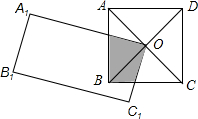 如图正方形ABCD的边长为2,对角线AC、BD相交于点O,点O又是长方形A1B1C1O的一个顶点,且OA1=4,OC1=2,使长方形绕点O转动过程中,长方形和正方形重叠部分的面积是1.
如图正方形ABCD的边长为2,对角线AC、BD相交于点O,点O又是长方形A1B1C1O的一个顶点,且OA1=4,OC1=2,使长方形绕点O转动过程中,长方形和正方形重叠部分的面积是1.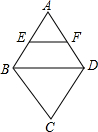 如图,在菱形ABCD中,∠BAD=60°,点E、F分别是AB、AD的中点,若S△AEF=4,则S五边形EBCDF=28.
如图,在菱形ABCD中,∠BAD=60°,点E、F分别是AB、AD的中点,若S△AEF=4,则S五边形EBCDF=28.