题目内容
1.如图1,在菱形ABCD中,对角线AC与BD交于点O,且AC=16,BD=12,现有两动点M、N分别从A、C同时出发,点M沿线段AB向终点B运动,点N沿折线C-D-A向终点A运动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为x(s).(1)填空:AB=10;S菱形ABCD=96;
(2)运动过程中,若点M的速度为每秒1个单位,点N的速度为每秒2个单位,连接AN、MN,记△AMN与△AOB的重叠部分面积为S,当点N运动到与直线AC的距离为1.8时,求S的值;
(3)运动过程中,若点M的速度为每秒1个单位,点N的速度为每秒a个单位(其中a<$\frac{10}{3}$),当x=6时在平面内存在点E使得以A、M、N、E为顶点的四边形为菱形,请求出所有满足条件的a的值.
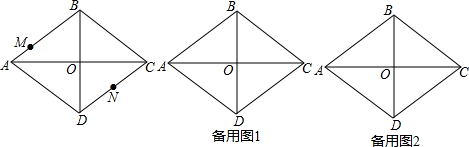
分析 (1)AB由勾股定理直接求出,菱形面积为对角线之积的一半.
(2)分两种情况:N在CD上和N在AD上.画出图形,找到重叠部分的几何形状.两种情况重叠部分都是三角形,因此算出各自的底和高即可.
(3)x=6,时间固定,AM的长度也就固定,A、M、N、E四点要形成菱形,分两大类情况,第一类以AM为边,这种情况可以画两种菱形;第二类以AM为对角线,只有一种.因此共三种情况,分别计算.
解答 解:(1)∵四边形ABCD是菱形,AC与BD交于点O,AC=16,BD=12,
∴AO=CO=8,BO=DO=6,AC⊥BD,
∴AB=10,
菱形ABCD的面积为$\frac{1}{2}$×12×16=96.
(2)①当N在CD上时,如图2-1所示,
过点N作NH⊥AC于H,则NH=1.8,过点M作MG⊥AC于G,连接MN交AC于点F,连接AN,
∵AB∥CD,
∴△AFM∽△CFN,
∵$\frac{CN}{AM}=\frac{2}{1}$,
∴$\frac{NH}{MG}=\frac{CF}{AF}=\frac{2}{1}$,
∴AF=$\frac{1}{3}$AC=$\frac{16}{3}$,
MG=$\frac{1}{2}$NH=0.9=$\frac{9}{10}$,
∴S△AMF=$\frac{1}{2}$×AF×MG=2.4.
②当N在AD上时,如图2-2所示,
过点N作NH⊥AC于H,则NH=1.8,过点M作MG⊥AC于G,连接MN交AC于点F,连接AN,
∵$\frac{AH}{AO}=\frac{AN}{AD}=\frac{NH}{OD}$
∴AN=3,AH=2.4,
t=$\frac{AD+CD-AN}{2}$=$\frac{17}{2}$,
∴AM=$\frac{17}{2}$,
∵$\frac{AG}{AO}=\frac{AM}{AB}=\frac{MG}{OB}$,
∴AG=6.8,MG=5.1,
∴GH=AG-AH=4.4,
∵$\frac{HF}{GF}=\frac{NH}{MG}=\frac{1.8}{5.1}=\frac{6}{17}$,
∴HF=$\frac{6}{23}$GH=$\frac{132}{115}$,
∴AF=AH+HF=2.4+$\frac{132}{115}$=$\frac{408}{115}$,
∴S△AMF=$\frac{1}{2}$×AF×MG=$\frac{1}{2}×\frac{408}{115}×\frac{51}{10}$=$\frac{5202}{525}$.
(3)x=6时,AM=6,
①如图3-1,四边形AMEN为菱形,
∴AN=AM=6,
∴ND+CD=20-6=14,
∴a=$\frac{14}{6}=\frac{7}{3}$.
②如图3-2,AENM为菱形,EM交AN于点R,作DP垂直BC于P,
∵菱形面积为96,
∴DP=9.6,
∴CP=2.8,
∴$\frac{AR}{AM}=\frac{CP}{CD}$,
∴AR=1.68,
∴AN=3.36,
∴a=(ND+CD)÷6=$\frac{208}{75}$,
③如图3-3,AEMN为菱形,EN交AM于点T,作BS垂直CD于S,
则AT=MT=3,
∴BT=NS=10-3=7,
∵BS=9.6,
∴CS=2.8,
∴CN=NS+CS=9.8,
∴a=CN÷6=$\frac{49}{30}$.
综上所述,a的取值有$\frac{7}{3}$、$\frac{208}{75}$、$\frac{49}{30}$.
点评 本题考查了菱形的性质、相似三角形的判定与性质、勾股定理、面积计算,分类讨论等重要知识点和技能,综合性和技巧性很强,计算量也较大,对学生的能力要求较高,是一道经典压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -13 | B. | 0 | C. | 2 | D. | 11 |
 已知有理数在数轴上的位置如图所示,则式子|a-c|-|a-b|+|2a|的化简结果是-b-c.
已知有理数在数轴上的位置如图所示,则式子|a-c|-|a-b|+|2a|的化简结果是-b-c.
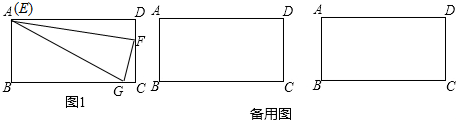
 如图,在Rt△ABC中,∠C=90,AC=3,BC=4,点E在直角边AC上(点E与A、C两点均不重合),点F在斜边AB上(点F与A、B两点均不重合).
如图,在Rt△ABC中,∠C=90,AC=3,BC=4,点E在直角边AC上(点E与A、C两点均不重合),点F在斜边AB上(点F与A、B两点均不重合).