题目内容
19.计算:(1)(-2)0+(-1)2010-($\frac{1}{2}$)-1
(2)先化简,再求值:($\frac{1}{m}-\frac{1}{n}$)÷$\frac{{m}^{2}-2mn+{n}^{2}}{mn}$,其中m=-3,n=5.
分析 (1)原式第一项利用零指数幂法则计算,第二项利用乘方的意义计算,最后一项利用负整数指数幂法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把m与n的值代入计算即可求出值.
解答 解:(1)原式=1+1-2=0;
(2)原式=$\frac{n-m}{mn}$•$\frac{mn}{(n-m)^{2}}$=$\frac{1}{n-m}$,
当m=-3,n=5时,原式=$\frac{1}{8}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知关于x的一元二次方程x2+x+m2-2m=0有一个实数根为-1,则m的值是( )
| A. | -1 | B. | 0 | C. | 2 | D. | 0或2 |
4.下列语句表示相反意义的量的是( )
| A. | 前进5米与前进8米 | B. | 盈利20元与亏损18元 | ||
| C. | 上升9℃与零下9℃ | D. | 收入10元与支出-10元 |
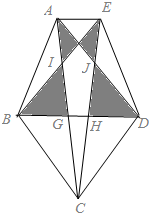 如图所示,三角形AEF,三角形BDF,三角形BCD都是正三角形,其中AE:BD=1:3,三角形AEF的面积是1,求阴影部分的面积.
如图所示,三角形AEF,三角形BDF,三角形BCD都是正三角形,其中AE:BD=1:3,三角形AEF的面积是1,求阴影部分的面积. 在网格中作出函数y=-2x+3的图象.根据图象回答:
在网格中作出函数y=-2x+3的图象.根据图象回答: