题目内容
9.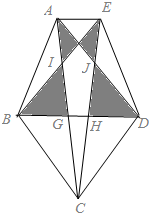 如图所示,三角形AEF,三角形BDF,三角形BCD都是正三角形,其中AE:BD=1:3,三角形AEF的面积是1,求阴影部分的面积.
如图所示,三角形AEF,三角形BDF,三角形BCD都是正三角形,其中AE:BD=1:3,三角形AEF的面积是1,求阴影部分的面积.
分析 设三角形AEF的边长为1份,根据其中两个等边三角形的边长的比确定其他各边的份数,从而表示出面积,然后利用四边形的蝴蝶定理确定各个三角形的面积,从而确定梯形ABCF的面积,进而可以确定阴影部分的面积.
解答 解:(1)设△AEF的边长为1份,
∵AE:BD=1:3,
∴△BDF和△BCD的边长都是3份.
(2)∵BF=3EF,∴△ABF的面积是△AEF的3倍,△ABF的面积等于1×3=3.
∵DF=3AF,∴△BDF的面积是△ABF的3倍,△BDF的面积等于3×3=9,
∴△BCD的面积也等于9.
(3)连接FC,整个图形关于FC对称,FC是对称轴.FC的左右两部分是相等的.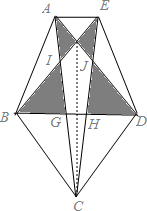 在梯形ABCF中,△ABF的面积是3,△BCF的面积为(9+9)÷2=9.
在梯形ABCF中,△ABF的面积是3,△BCF的面积为(9+9)÷2=9.
梯形ABCF的面积是3+9=12,
而这个梯形的上底是1份,下底是3份.
根据四边形的蝴蝶定理:
△AIF:△BCI:△ABI:△FIC=12:32:3:3=1:9:3:3,
∵梯形ABCF的面积是12,梯形ABCF又被分成了1+9+3+3=16份,而阴影部分只占其中的1+9=10份.
∴梯形ABCF中的阴影部分的面积是12×$\frac{1+9}{1+9+3+3}$=$\frac{15}{2}$,
∴整个图形中的阴影部分的面积是$\frac{15}{2}$×2=15.
点评 本题考查了面积及面积变换的问题,解题的关键是了解四边形蝴蝶定理的相关内容:相似图形,面积比等于对应边长比的平方,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列变形属于移项的是( )
| A. | 由-$\frac{1}{4}$x=2,得x=-8 | B. | 由8x+7=3,得8x+7-6=3-6 | ||
| C. | 由8=-5x+2,得5x=2-8 | D. | 由$\frac{11}{6}$=-2a,得-2a=$\frac{11}{6}$ |
18.一元二次方程5x2-1=4x的二次项系数是( )
| A. | -1 | B. | 1 | C. | 4 | D. | 5 |
 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x( m)之间的关系为y=-$\frac{1}{9}$(x-4)2+4,由此可知铅球推出的距离是10m.
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x( m)之间的关系为y=-$\frac{1}{9}$(x-4)2+4,由此可知铅球推出的距离是10m.