题目内容
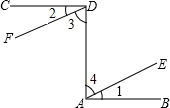如图，已知CD⊥DA，AB⊥DA，∠1=∠2，试判断直线DF与AE关系，并说明理由．考点：平行线的判定
专题：
分析：根据垂直定义可得∠CDA=∠DAB=90°，再根据等角的余角相等可得∠3=∠4，再根据内错角相等，两直线平行可直接证出结论．
解答：DF∥AE，
证明：∵CD⊥DA于点D，AB⊥DA于点A，
∴∠CDA=∠DAB=90°，
∵∠1=∠2．
∴∠3=∠4，
∴DF∥AE．
证明：∵CD⊥DA于点D，AB⊥DA于点A，
∴∠CDA=∠DAB=90°，
∵∠1=∠2．
∴∠3=∠4，
∴DF∥AE．
点评：此题主要考查了平行线的判定，关键是掌握内错角相等两直线平行的知识．
练习册系列答案
春雨教育同步作文系列答案
相关题目
永川到成都路程全长288km，一辆小汽车和一辆客车同时从永川、成都两地相向而行，经过1小时50分钟相遇，相遇时小汽车比客车多行驶40km．设小汽车和客车的平均速度为x km/h和y km/h，则下列方程组正确的是（ ）
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
下列命题是真命题的个数（ ）
（1）反比例函数y=
的图象，y随x的增大而减小；
（2）（a-3）0=1；
（3）函数xy=k是反比例函数；
（4）一组数0.3，0.4，0.5这组数是勾股数．
（1）反比例函数y=
| 3 |
| x |
（2）（a-3）0=1；
（3）函数xy=k是反比例函数；
（4）一组数0.3，0.4，0.5这组数是勾股数．
| A、0个 | B、1个 | C、2个 | D、3个 |
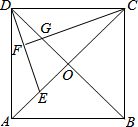如图，已知正方形ABCD中，AC、BD相交于点O，E是OA上一点，CF分别交BD、ED于点G、F，且OG=OE．问CG与DE有怎样的关系？试证明你的结论．（提示：关系有位置关系与数量关系）