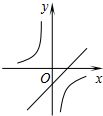题目内容
20. 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
分析 (1)根据旋转中心方向及角度找出点A、B的对应点A1、B1的位置,然后顺次连接即可,根据A、B的坐标建立坐标系,据此写出点A1、B1的坐标;
(2)利用勾股定理求出AC的长,根据△ABC扫过的面积等于扇形CAA1的面积与△ABC的面积和,然后列式进行计算即可.
解答 解:(1)所求作△A1B1C如图所示:
由A(4,3)、B(4,1)可建立如图所示坐标系,
则点A1的坐标为(-1,4),点B1的坐标为(1,4);
(2)∵AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,∠ACA1=90°
∴在旋转过程中,△ABC所扫过的面积为:
S扇形CAA1+S△ABC
=$\frac{90π•(\sqrt{13})^{2}}{360}$+$\frac{1}{2}$×3×2
=$\frac{13π}{4}$+3.
点评 本题考查了利用旋转变换作图,熟练掌握网格结构,准确找出对应点位置作出图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.如图,是由若干个大小相同的正方体搭成的几何体的三视图,该几何体所用的正方体的个数是( )


| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
5.姜老师给出一个函数表达式,甲、乙、丙三位同学分别正确指出了这个函数的一个性质.甲:函数图象经过第一象限;乙:函数图象经过第三象限;丙:在每一个象限内,y值随x值的增大而减小.根据他们的描述,姜老师给出的这个函数表达式可能是( )
| A. | y=3x | B. | $y=\frac{3}{x}$ | C. | $y=-\frac{1}{x}$ | D. | y=x2 |
12.下列运算正确的是( )
| A. | x3+x2=x5 | B. | a3•a4=a12 | C. | (-x3)2÷x5=1 | D. | (-xy)3•(-xy)-2=-xy |
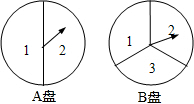 小明和小亮用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于2,则小明胜,否则小亮胜.这个游戏对双方公平吗?请说明理由.
小明和小亮用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于2,则小明胜,否则小亮胜.这个游戏对双方公平吗?请说明理由. 如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( )
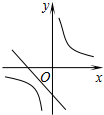
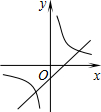
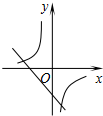
如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( )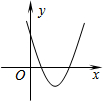 二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数$y=-\frac{a}{x}$与一次函数y=bx-c在同一坐标系内的图象大致是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数$y=-\frac{a}{x}$与一次函数y=bx-c在同一坐标系内的图象大致是( )