题目内容
12.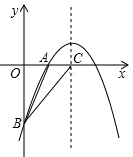 如图,已知二次函数y=-$\frac{1}{2}$x2+bx-6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
如图,已知二次函数y=-$\frac{1}{2}$x2+bx-6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
分析 由点A的坐标利用待定系数法即可求出二次函数解析式,根据二次函数的解析式即可找出抛物线的对称轴,从而得出点C的坐标,再将x=0代入二次函数解析式求出点B的坐标,利用三角形的面积公式即可得出结论.
解答 解:将A(2,0)代入函数y=-$\frac{1}{2}$x2+bx-6,
得:0=-2+2b-6,解得:b=4,
∴二次函数解析式为y=-$\frac{1}{2}$x2+4x-6.
当x=0时,y=-6,
∴B(0,-6),
抛物线对称轴为x=-$\frac{b}{2a}$=4,
∴C(4,0),
∴S△ABC=$\frac{1}{2}$AC•OB=$\frac{1}{2}$×(4-2)×6=6.
点评 本题考查了待定系数法求二次函数解析式以及二次函数图象上点的坐标特征,根据点的坐标利用待定系数法求出函数解析式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.数轴上的点M对应的数是-2,点N与点M距离4个单位长度,此时点N表示的数是( )
| A. | -6 | B. | 2 | C. | -6或2 | D. | 都不正确 |
 已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.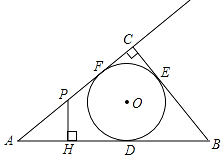 如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.
如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.