题目内容
7.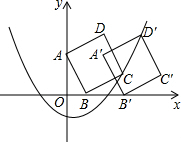 如图,在平面直角坐标系中,正方形ABCD的顶点A,B的坐标分别为(0,2),(1,0),顶点C在函数y=$\frac{1}{3}$x2+bx-1的图象上,将正方形ABCD沿x轴正方形平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′间的距离为2.
如图,在平面直角坐标系中,正方形ABCD的顶点A,B的坐标分别为(0,2),(1,0),顶点C在函数y=$\frac{1}{3}$x2+bx-1的图象上,将正方形ABCD沿x轴正方形平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′间的距离为2.
分析 作辅助线,构建全等三角形,先根据A和B的坐标求OB和OA的长,证明∴△AOB≌△BGC,BG=OA=2,CG=OB=1,写出C(3,1),同理得:△BCG≌△CDH,得出D的坐标,根据平移的性质:D与D′的纵坐标相同,则y=3,求出D′的坐标,计算其距离即可.
解答 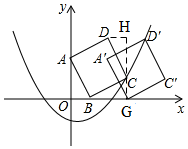 解:如图,过C作GH⊥x轴,交x轴于G,过D作DH⊥GH于H,
解:如图,过C作GH⊥x轴,交x轴于G,过D作DH⊥GH于H,
∵A(0,2),B(1,0),
∴OA=2,OB=1,
∵四边形ABCD为正方形,
∴∠ABC=90°,AB=BC,
∴∠ABO+∠CBG=90°,
∵∠ABO+∠OAB=90°,
∴∠CBG=∠OAB,
∵∠AOB=∠BGC=90°,
∴△AOB≌△BGC,
∴BG=OA=2,CG=OB=1,
∴C(3,1),
同理得:△BCG≌△CDH,
∴CH=BG=2,DH=CG=1,
∴D(2,3),
∵C在抛物线的图象上,
把C(3,1)代入函数y=$\frac{1}{3}$x2+bx-1中得:b=-$\frac{1}{3}$,
∴y=$\frac{1}{3}$x2-$\frac{1}{3}$x-1,
设D(x,y),
由平移得:D与D′的纵坐标相同,则y=3,
当y=3时,$\frac{1}{3}$x2-$\frac{1}{3}$x-1=3,
解得:x1=4,x2=-3(舍),
∴DD′=4-2=2,
则点D与其对应点D′间的距离为2,
故答案为:2.
点评 本题考查出了二次函数图象与几何变换--平移、三角形全等的性质和判定、正方形的性质,作辅助线,构建全等三角形,明确D与D′的纵坐标相同是关键.

练习册系列答案
相关题目
15.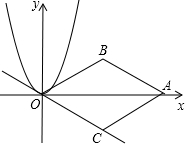 如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )
如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )
 如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )
如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )| A. | $\sqrt{3}$≤m≤3$\sqrt{3}$ | B. | 3$\sqrt{3}$≤m≤$\frac{10}{3}$$\sqrt{3}$ | C. | $\frac{10}{3}$$\sqrt{3}$≤m≤$\frac{16}{3}$$\sqrt{3}$ | D. | $\sqrt{3}$≤m≤$\frac{16}{3}$$\sqrt{3}$ |
2.如果关于x的一元二次方程x2-6x+m=0有两个相等的实数根,则m所满足的条件是( )
| A. | m<9 | B. | m>9 | C. | m=9 | D. | m≤9 |
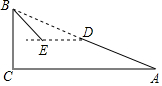 如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,
如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,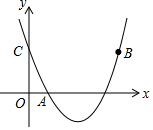 如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点A的坐标为(1,0),点B是点C关于该函数图象对称轴对称的点.
如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点A的坐标为(1,0),点B是点C关于该函数图象对称轴对称的点.