题目内容
19. 你能证明你所得出的结论吗?
你能证明你所得出的结论吗?(1)证明线段、角相等的一般方法是利用三角形全等,怎样构造三角形.
(2)由平行四边形的定义及AC是公共边.易得△ABC≌△CDA
(3)由此可得到哪些相等的线段、角?
结论:平行四边形的性质:AB=CD,BC=AD;∠B=∠D,∠BAD=∠BCD,
请你数学几何语言给平行四边形的性质:平行四边形的对边相等,平行四边形的对角相等.
分析 连接AC.根据ASA证明△ABC≌△CDA即可解决问题.
解答 解:如图连接AC.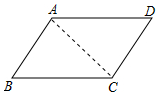
∵四边形ABCD是平行四边形,
∵AB∥CD,AD∥BC,
∴∠BADBAC=∠ACD,∠BCA=∠CAD,
在△ABC和△CDA中,
$\left\{\begin{array}{l}{∠BAC=∠ACD}\\{AC=CA}\\{∠BCA=∠CAD}\end{array}\right.$,
∴△ABC≌△CDA,
∴AB=CD,BC=AD,∠B=∠D,
∵∠BAC=∠ACD,∠BCA=∠CAD,
∠BAD=∠BCD.
故答案分别为≌,AB=CD,BC=AD;∠B=∠D,∠BAD=∠BCD;平行四边形的对边相等,平行四边形的对角相等.
点评 本题考查全等三角形的判定和性质、平行四边形的判定和性质等知识,解题的关键是学会用转化的思想思考问题,把四边形问题转化为三角形问题,属于中考常考题型.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
10. 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )| A. | a-c>b-c | B. | $\frac{a}{b}$<$\frac{c}{b}$ | C. | ac>bc | D. | a+c<b+c |
7.下列四个数中,绝对值最大的是( )
| A. | 2 | B. | 0 | C. | -$\frac{1}{3}$ | D. | -3 |
14.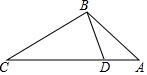 如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
 如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )| A. | ∠ABD=∠C | B. | ∠ADB=∠ABC | C. | $\frac{AB}{BD}=\frac{CB}{CA}$ | D. | $\frac{AB}{AD}=\frac{AC}{AB}$ |
4.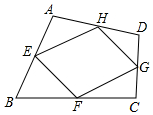 如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
 如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )| A. | 20 | B. | 28 | ||
| C. | 14 | D. | 以上答案均有可能 |
9.要得到二次函数y=-x2+2x的图象,需将二次函数y=-x2的图象( )
| A. | 向左平移1个单位,再向上平移1个单位 | |
| B. | 向右平移1个单位,再向下平移1个单位 | |
| C. | 向左平移1个单位,再向下平移1个单位 | |
| D. | 向右平移1个单位,再向上平移1个单位 |
 如图是一个正方体纸盒的展开图,请把-10,7,10,-2,-7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
如图是一个正方体纸盒的展开图,请把-10,7,10,-2,-7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数. 如图,直线AB,CD相交于O,OE平分∠AOD,∠FOC=100°,∠1=40°,求∠2和∠3的度数.
如图,直线AB,CD相交于O,OE平分∠AOD,∠FOC=100°,∠1=40°,求∠2和∠3的度数.