题目内容
如图，∠A＝∠D，AC＝DF，那么需要补充一个直接条件________(写出一个即可)，才能使△ABC≌△DEF．
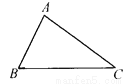
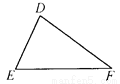
AB＝DE（或∠B＝∠E或∠C＝∠F）
【解析】添加条件AB=DE，
在△ABC和△DEF中，
，
∴△ABC≌△DEF(SAS)；
或添加条件∠B＝∠E，
在△ABC和△DEF中， ，
∴△ABC≌△DEF(AAS)；
或添加条件∠C＝∠F，
在△ABC和△DEF中， ，
∴△ABC≌△DEF(ASA)；
故答案为：AB=DE（或...
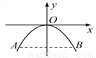
备战中考寒假系列答案如图，有一抛物线拱桥，当水位线在AB位置时，拱桥顶离水面2m，水面宽4m，水面下降1m后，水面宽为( )
A. 5m B. 6m C.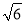 
m D. 2
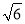m
D
【解析】试题分析：建立如图所示的坐标系，则点A的坐标为（-2，-2），设函数关系式为，则-2=4a，所以a= -，所以，当y=-3时， ，所以水面宽为m，故选：D． 根据下列表格对应值：
x | 3 | 4 | 5 |
y=ax2+bx+c | 0.5 | ﹣0.5 | ﹣1 |
判断关于x的方程ax2+bx+c=0（a≠0）的一个解x的范围是（ ）
A. x＜3 B. x＞5 C. 3＜x＜4 D. 4＜x＜5
C
【解析】试题分析：∵x=3时，y=0.5，即ax2+bx+c＞0；
x=4时，y=﹣0.5，即ax2+bx+c＜0，
∴抛物线与x轴的一个交点在（3，0）和（4，0）之间，
∴关于x的方程ax2+bx+c=0（a≠0）的一个解x的范围是3＜x＜4．
故选C． 如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（ ）
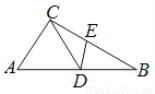
A. 50° B. 51° C. 51.5° D. 52.5°
D
【解析】试题分析：根据等腰三角形的性质推出∠A=∠CDA=50°，∠B=∠DCB，∠BDE=∠BED，根据三角形的外角性质求出∠B=25°，由三角形的内角和定理求出∠BDE=∠BED=（180°﹣25°）=77.5°，，根据平角的定义即可求出∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°，故答案选D． 每一个多边形都可以按图的方法割成若干个三角形．而每一个三角形的三个内角的和是180°．按图的方法，十二边形的内角和是__________度．
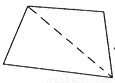
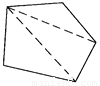
1800
【解析】∵过四边形的一个顶点可画一条对角线，将四边形分成两个三角形，
过五边形的一个顶点可画两条对角线，将五边形分成三个三角形，
过六边形的一个顶点可画三条对角线，将六边形分成四个三角形，
∴过十二边形的一个顶点可画九条对角线，将十二边形分成十个三角形，
而三角形的内角和等于180°，
∴十二边形的内角和是180°×10=1800°.
故答案为：... 三条线段长度分别为3、4、6，则以此三条线段为边所构成的三角形按角分类是 ( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 根本无法确定
C
【解析】∵32+42=25，∴以3、4为直角边的三角形的斜边为5，
∵5<6，∴以3、4、6为三边构成的三角形是钝角三角形.
故选：C. 在锐角三角形中，最大角α的取值范围是 ( )
A. 0°＜α＜90° B. 60°＜α＜90° C. 60°＜α＜180° D. 60°≤α＜90°
D
【解析】三角形三个内角的和等于180°，设其他两个角分别为β和γ，由题意α<90°，α?β且α?γ，α+β+γ=180°，所以3α?180°，即α?60°.
故选：D. 如图，抛物线y=﹣x2+3x+4与x轴交于点A，B，与y轴交于点C，P（m，n）为第一象限内抛物线上的一点，点D的坐标为（0，6）．
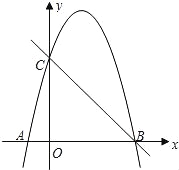
（1）OB=_________，抛物线的顶点坐标为_________________；
（2）当n=4时，求点P关于直线BC的对称点P′的坐标；
（3）是否存在直线PD，使直线PD所对应的一次函数随x的增大而增大？若存在，直接写出m的取值范围；若不存在，请说明理由．
（1）4，（，）；（2）（0，1）；（3）1＜m＜2．
【解析】
试题分析：（1）当y=0时，即﹣x2+3x+4=0，解得：x1=4，x2=﹣1，∴点A（﹣1，0）点B（4，0），∴OB=4，y=﹣x2+3x+4=，∴抛物线的顶点坐标为（，），故答案为：4，（，）．
（2）如图，连接CP，CP′，
n=4时，﹣m2+3m+4=4，解得：m1=3，m2=0（舍去），∴这时P点... 关于二次函数y=x2﹣2x﹣3的图象，下列说法中错误的是（ ）
A. 当x＜2，y随x的增大而减小 B. 函数的对称轴是直线x=1
C. 函数的开口方向向上 D. 函数图象与y轴的交点坐标是（0，﹣3）
A
【解析】试题分析：∵y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴抛物线开口向上，对称轴为x=1，当x＜1时y随x的增大而减小，故B、C正确，A不正确，
令x=0可得y=﹣3，
∴抛物线与y轴的交点坐标为（0，﹣3），故D正确，
故选A．