题目内容
三条线段长度分别为3、4、6,则以此三条线段为边所构成的三角形按角分类是 ( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 根本无法确定
 C
【解析】∵32+42=25,∴以3、4为直角边的三角形的斜边为5,
∵5<6,∴以3、4、6为三边构成的三角形是钝角三角形.
故选:C.
C
【解析】∵32+42=25,∴以3、4为直角边的三角形的斜边为5,
∵5<6,∴以3、4、6为三边构成的三角形是钝角三角形.
故选:C.
 应用题作业本系列答案
应用题作业本系列答案如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是_________;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是____________.
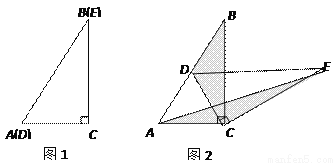
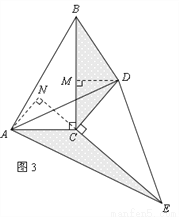
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE//AB交BC于点E(如图4).若在射线BA上存在点F,使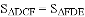 ,请直接写出相应的BF的长.
,请直接写出相应的BF的长.

 (1)①DE∥AC;②S1=S2;(2)证明见解析;(3)BF的长为或.
【解析】试题分析:(1)①根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行解答;
②根据等边三角形的性质可得AC=AD,再根据直角三角形30°角所对的直角边等于斜边的一半求出AC=AB,然后求出AC=BD,再根据等边三角形的性质求...
(1)①DE∥AC;②S1=S2;(2)证明见解析;(3)BF的长为或.
【解析】试题分析:(1)①根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行解答;
②根据等边三角形的性质可得AC=AD,再根据直角三角形30°角所对的直角边等于斜边的一半求出AC=AB,然后求出AC=BD,再根据等边三角形的性质求... 函数y=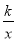 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A. 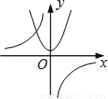 B.
B. 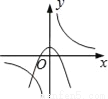 C.
C. 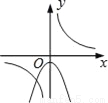 D.
D. 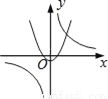
 B
【解析】A选项中,若反比例函数如图,则,那么抛物线应与y轴交于负半轴,所以A不可能;
B选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以B可能;
C选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以C不可能;
D选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以D不可能;
故选B.
...
B
【解析】A选项中,若反比例函数如图,则,那么抛物线应与y轴交于负半轴,所以A不可能;
B选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以B可能;
C选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以C不可能;
D选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以D不可能;
故选B.
... 已知:如图,在△ABC中,∠ACB=90°,CD为高,CE平分∠BCD,且∠ACD:∠BCD=1:2,那么CE是AB边上的中线对吗?说明理由.
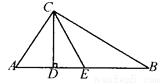
 见解析
【解析】试题分析:先求出∠ACD=30°,∠BCD=60°,然后根据角平分线的定义求出∠DCE=∠BCE=30°,再根据直角三角形两锐角互余求出∠B,∠A,从而得到∠A=∠ACE,∠B=∠BCE,根据等角对等边的性质可得AE=EC,BE=EC,然后求出AE=BE,即可得解.
试题解析:CE是AB边上的中线。
理由:∵∠ACB=90°,∠ACD:∠BCD=1:2,
∴...
见解析
【解析】试题分析:先求出∠ACD=30°,∠BCD=60°,然后根据角平分线的定义求出∠DCE=∠BCE=30°,再根据直角三角形两锐角互余求出∠B,∠A,从而得到∠A=∠ACE,∠B=∠BCE,根据等角对等边的性质可得AE=EC,BE=EC,然后求出AE=BE,即可得解.
试题解析:CE是AB边上的中线。
理由:∵∠ACB=90°,∠ACD:∠BCD=1:2,
∴... 如图,∠A=∠D,AC=DF,那么需要补充一个直接条件________(写出一个即可),才能使△ABC≌△DEF.
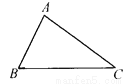
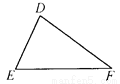
 AB=DE(或∠B=∠E或∠C=∠F)
【解析】添加条件AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
或添加条件∠B=∠E,
在△ABC和△DEF中, ,
∴△ABC≌△DEF(AAS);
或添加条件∠C=∠F,
在△ABC和△DEF中, ,
∴△ABC≌△DEF(ASA);
故答案为:AB=DE(或...
AB=DE(或∠B=∠E或∠C=∠F)
【解析】添加条件AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
或添加条件∠B=∠E,
在△ABC和△DEF中, ,
∴△ABC≌△DEF(AAS);
或添加条件∠C=∠F,
在△ABC和△DEF中, ,
∴△ABC≌△DEF(ASA);
故答案为:AB=DE(或... 等腰三角形的周长为24cm,腰长为xcm,则x的取值范围是( )
A. x<6 B. 6<x<12 C. 0<x<12 D. x>12
 B
【解析】等腰三角形的周长为24cm,腰长为xcm,则底边长为24-2x,
根据三边关系,x+x>24-2x,解得,x>6;
x-x<24-2x,解得,x<12,
所x的取值范围是6<x<12.
故选:C.
B
【解析】等腰三角形的周长为24cm,腰长为xcm,则底边长为24-2x,
根据三边关系,x+x>24-2x,解得,x>6;
x-x<24-2x,解得,x<12,
所x的取值范围是6<x<12.
故选:C. 分解因式:x2(x-y)2-4(y-x)2.
 (x-y)2(x+2)(x-2)
【解析】试题分析:提取公因式(x-y)2后,再利用平方差公式因式分解即可.
试题解析:
x2(x-y)2-4(y-x)2
=x2(x-y)2-4(x-y)2
=(x-y)2(x2-4)
=(x-y)2(x+2)(x-2).
(x-y)2(x+2)(x-2)
【解析】试题分析:提取公因式(x-y)2后,再利用平方差公式因式分解即可.
试题解析:
x2(x-y)2-4(y-x)2
=x2(x-y)2-4(x-y)2
=(x-y)2(x2-4)
=(x-y)2(x+2)(x-2). 如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线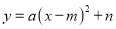 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为_______。
的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为_______。
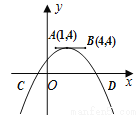
 8
【解析】当抛物线y=a(x-m)2+n的顶点在线段AB的A点上时,点C的横坐标最小,把A(1,4)代入得:y=a(x-1)2+4,把C(-3,0)代入得:0=a(-3-1)2+4,解得:a=-,即:y=-(x-1)2+4,再根据题意知抛物线y=a(x-m)2+n的顶点在线段AB上运动,可得抛物线的a永远等于-,当抛物线的顶点运动到B时,D的横坐标最大,把a=-和B(4,4)代入y=a(x...
8
【解析】当抛物线y=a(x-m)2+n的顶点在线段AB的A点上时,点C的横坐标最小,把A(1,4)代入得:y=a(x-1)2+4,把C(-3,0)代入得:0=a(-3-1)2+4,解得:a=-,即:y=-(x-1)2+4,再根据题意知抛物线y=a(x-m)2+n的顶点在线段AB上运动,可得抛物线的a永远等于-,当抛物线的顶点运动到B时,D的横坐标最大,把a=-和B(4,4)代入y=a(x... 已知2a-3x+1=0,3b-2x-16=0,且a≤4<b,求x的取值范围.
 【解析】【解析】
由已知得:a=,b=
又∵a≤4<b
∴
解此不等式组,得
-2<x≤3.
【解析】【解析】
由已知得:a=,b=
又∵a≤4<b
∴
解此不等式组,得
-2<x≤3. 
