题目内容
5.函数可揭示事物变化规律,它有多种表示形式.如表格、图象、表达式等,这些表示形式各有优势.图象法直观、列表法具体、表达式精确.若把三者结合起来,则能更全而深刻地理解变量之间的关系.试解决下列问题.(1)已知函数表达式y=$\frac{2}{{x}^{2}}$,你能说出它的图象具有的一些特征吗?试画出它的图象:
(2)试说明下列函数的图象与y=$\frac{2}{{x}^{2}}$的图象之间的位置关系,并在同一平面直角坐标系中画出它们的图象.
①y=$\frac{2}{{x}^{2}}$-2
②y=$\frac{2}{(x-1)^{2}}$.
分析 (1)根据函数的解析式作出函数的图象,然后描述其所处的位置及其增减性即可;
(2)根据函数图象平移规律:左加右减上加下减,可得答案.
解答 解:(1)函数y=$\frac{2}{{x}^{2}}$的图象如下图: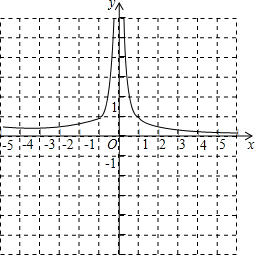
函数的图象是双曲线,两个分支分别位于一、二象限,在第二象限y随着x的增大而增大,在第一象限y随着x的增大而减小;
(2)如图:
y=$\frac{2}{{x}^{2}}$的图象向下平移两个单位得①y=$\frac{2}{{x}^{2}}$-2
y=$\frac{2}{{x}^{2}}$的图象向右平移一个单位得y=$\frac{2}{(x-1)^{2}}$.
点评 本题考查了反比例函数的图象及性质,解题的关键是正确的作出反比例函数的图象,难度不大.

练习册系列答案
相关题目
16. 如图所示,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中等腰三角形有( )
如图所示,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中等腰三角形有( )
 如图所示,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中等腰三角形有( )
如图所示,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中等腰三角形有( )| A. | 3个 | B. | 5个 | C. | 7个 | D. | 8个 |
 有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|a|+|b|.
有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|a|+|b|. 有理数a,b,c在数轴上如图所示,试化简|2c-b|+|a+b|-|2a-c|.
有理数a,b,c在数轴上如图所示,试化简|2c-b|+|a+b|-|2a-c|.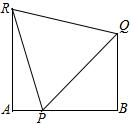 设在一条小巷内,∠A=∠B=90°,一个梯子的底脚位于点P处,当该梯子顶端靠在小巷一侧的墙上点Q时,梯子的倾斜角为45°,当顶端靠在小巷的另一侧墙上时,其顶端R离开地面高度为4米,且此时梯子的倾斜角为75°.
设在一条小巷内,∠A=∠B=90°,一个梯子的底脚位于点P处,当该梯子顶端靠在小巷一侧的墙上点Q时,梯子的倾斜角为45°,当顶端靠在小巷的另一侧墙上时,其顶端R离开地面高度为4米,且此时梯子的倾斜角为75°.
 如图所示,A是直线上的一个点,请你在A点的右侧每隔1厘米取一个点,共取三个点,那么
如图所示,A是直线上的一个点,请你在A点的右侧每隔1厘米取一个点,共取三个点,那么