题目内容
抛物线y=-x2+bx+c与x轴交于A(1,0)、B(-3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的第二象限内是否存在点P,使得△PBC的面积等于△OBC的一半?若存在,求出P点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的对称轴上是否存在一点Q,使△QBC为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的第二象限内是否存在点P,使得△PBC的面积等于△OBC的一半?若存在,求出P点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的对称轴上是否存在一点Q,使△QBC为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)把A(1,0)、B(-3,0)两点代入抛物线y=-x2+bx+c得
,再求出方程组的解即可,
(2)设P点(x,-x2-2x+3)(-3<x<0),根据S△BPC=S△BPE+S直角梯形PEOC-S△BOC得出S△BPC=-
(x+
)2+
,再根据△PBC的面积等于△OBC的一半,得出-
(x+
)2+
=
×
,再解方程即可,
(3)若∠CBQ=90°,设BQ与y轴交与点M,求出BM与抛物线的交点,得出点Q1的坐标,若∠BCQ=90°,设CQ与x轴交与点N,求出BN与抛物线的交点,得出点Q2的坐标,若∠BQD=90°,先求出以BC为直径的方程是(x+
)2+(y-
)2=
,由求出
的解即可得出点Q3和点Q4的坐标.
|
(2)设P点(x,-x2-2x+3)(-3<x<0),根据S△BPC=S△BPE+S直角梯形PEOC-S△BOC得出S△BPC=-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
| 1 |
| 2 |
| 9 |
| 2 |
(3)若∠CBQ=90°,设BQ与y轴交与点M,求出BM与抛物线的交点,得出点Q1的坐标,若∠BCQ=90°,设CQ与x轴交与点N,求出BN与抛物线的交点,得出点Q2的坐标,若∠BQD=90°,先求出以BC为直径的方程是(x+
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
|
解答:解:(1)∵抛物线y=-x2+bx+c与x轴交于A(1,0)、B(-3,0)两点,
∴
解得:
∴该抛物线的解析式为:y=-x2-2x+3;
(2)如图:设P点(x,-x2-2x+3)(-3<x<0)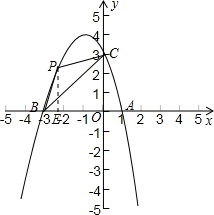
则S△BPC=S△BPE+S直角梯形PEOC-S△BOC
=
BE•PE+
OE(PE+OC)-
=
(x+3)(-x2-2x+3)+
(-x)(-x2-2x+3+3)-
=-
(x+
)2+
,
若△PBC的面积等于△OBC的一半,
则-
(x+
)2+
=
×
解得:x1=
,x2=
,
当x=
时,y=
<3,不合题意舍去,
当x=
时,y=
,
则P点的坐标是(
,
);
(3)如图:若∠CBQ=90°,设BQ与y轴交与点M,
则BM的解析式为:y=-x-3,
由
得;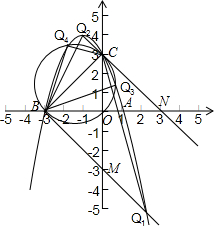
(舍去)或
,
则点Q1的坐标是:(2,-5),
若∠BCQ=90°,设CQ与x轴交与点N,
则CN的解析式为:y=-x+3,
由
得;
(舍去)或
,
则点Q2的坐标是:(-1,4),
若∠BQD=90°,
∵以BC为直径的方程是(x+
)2+(y-
)2=
,
由
得;
(舍去),
(舍去),
,
,
∴若∠BQD=90°,点Q3的坐标是(
,
)或点Q4的坐标是(
,
).
∴
|
解得:
|
∴该抛物线的解析式为:y=-x2-2x+3;
(2)如图:设P点(x,-x2-2x+3)(-3<x<0)
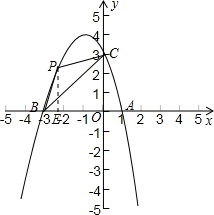
则S△BPC=S△BPE+S直角梯形PEOC-S△BOC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
若△PBC的面积等于△OBC的一半,
则-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
| 1 |
| 2 |
| 9 |
| 2 |
解得:x1=
| ||
| 2 |
-
| ||
| 2 |
当x=
| ||
| 2 |
| 9 |
| 4 |
当x=
-
| ||
| 2 |
| 9 |
| 4 |
则P点的坐标是(
-
| ||
| 2 |
| 9 |
| 4 |
(3)如图:若∠CBQ=90°,设BQ与y轴交与点M,
则BM的解析式为:y=-x-3,
由
|

|
|
则点Q1的坐标是:(2,-5),
若∠BCQ=90°,设CQ与x轴交与点N,
则CN的解析式为:y=-x+3,
由
|
|
|
则点Q2的坐标是:(-1,4),
若∠BQD=90°,
∵以BC为直径的方程是(x+
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
由
|
|
|
|
|
∴若∠BQD=90°,点Q3的坐标是(
-1+
| ||
| 2 |
5-
| ||
| 2 |
-1-
| ||
| 2 |
5+
| ||
| 2 |
点评:此题考查了二次函数的综合应用,用到的知识点是三角形、梯形的面积公式、一次函数、二次函数的图象和性质,关键是根据题意画出图形,把不合题意得解舍去,注意数形结合思想和分类讨论思想的应用.

练习册系列答案
相关题目
若点A(3-m,n+2)关于原点的对称点B的坐标是(-3,2),则m,n的值为( )
| A、m=-6,n=-4 |
| B、m=O,n=-4 |
| C、m=6,n=4 |
| D、m=6,n=-4 |
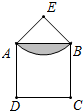 如图所示,△EBA是等边三角形,□ABCD边长为6,E是过A、B两点圆弧的圆心,求阴影部分面积.
如图所示,△EBA是等边三角形,□ABCD边长为6,E是过A、B两点圆弧的圆心,求阴影部分面积.