题目内容
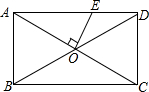 如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE⊥AC交AD于点E,则AE的长是
如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE⊥AC交AD于点E,则AE的长是考点:矩形的性质,线段垂直平分线的性质,勾股定理
专题:
分析:连接CE,根据矩形的对边相等可得AD=BC=8,CD=AB=4,根据矩形的对角线互相平分可得OA=OC,然后判断出OE垂直平分AC,再根据线段垂直平分线上的点到两端点的距离相等可得AE=CE,设AE=CE=x,表示出DE,然后在Rt△CDE中,利用勾股定理列出方程求解即可.
解答: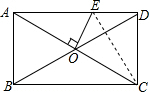 解:如图,∵矩形ABCD中,AB=3,BC=5,
解:如图,∵矩形ABCD中,AB=3,BC=5,
∴AD=BC=8,CD=AB=8,OA=OC,
∵OE⊥AC,
∴OE垂直平分AC,
∴AE=CE,
设AE=CE=x,则DE=8-x,
在Rt△CDE中,CD2+DE2=CE2,
即42+(8-x)2=x2,
解得x=5,
即AE的长为5.
故答案为:5.
 解:如图,∵矩形ABCD中,AB=3,BC=5,
解:如图,∵矩形ABCD中,AB=3,BC=5,∴AD=BC=8,CD=AB=8,OA=OC,
∵OE⊥AC,
∴OE垂直平分AC,
∴AE=CE,
设AE=CE=x,则DE=8-x,
在Rt△CDE中,CD2+DE2=CE2,
即42+(8-x)2=x2,
解得x=5,
即AE的长为5.
故答案为:5.
点评:本题考查了矩形的性质,线段垂直平分线上的点到两端点的距离相等的性质,勾股定理,熟记各性质并利用勾股定理列出方程是解题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
下列计算正确的是( )
| A、(-0.01)-2=10000 | ||
B、-10-2=
| ||
C、
| ||
D、2a-2=
|
 如图,在△ABC中,D为BC上一点,DE∥AC交AB于E点,DF∥AB交AC于F点,当AD满足条件
如图,在△ABC中,D为BC上一点,DE∥AC交AB于E点,DF∥AB交AC于F点,当AD满足条件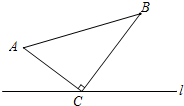 如图,△ABC中,∠ACB=90°,AC=7cm,BC=1lcm.点M从A点出发沿A→C→B路径向终点运动,终点为B点;点N从B点出发沿B→C→A路径向终点运动,终点为A点.点M和N分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,则当t=
如图,△ABC中,∠ACB=90°,AC=7cm,BC=1lcm.点M从A点出发沿A→C→B路径向终点运动,终点为B点;点N从B点出发沿B→C→A路径向终点运动,终点为A点.点M和N分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,则当t=