题目内容
2.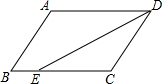 如图,在?ABCD中,已知AD=10cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE=4cm.
如图,在?ABCD中,已知AD=10cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE=4cm.
分析 根据平行四边形的性质得出AB=CD=6cm,AD=BC=10cm,AD∥BC,根据平行线的性质得出∠ADE=∠CED,求出∠CDE=∠CED,根据等腰三角形的判定得出DC=EC,即可求出答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD=6cm,AD=BC=10cm,AD∥BC,
∴∠ADE=∠CED,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CDE=∠CED,
∴DC=EC=6cm,
∴BE=BC-CE=10cm-6cm=4cm,
故答案为:4cm.
点评 本题主要考查对平行四边形性质的理解和掌握,能熟练地运用性质求出BC和CE的长是解此题的关键,注意:平行四边形的对边平行且相等.

练习册系列答案
相关题目
13.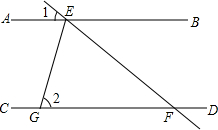 如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF交CD于点G.若∠1=36°,则∠2的大小是( )
如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF交CD于点G.若∠1=36°,则∠2的大小是( )
 如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF交CD于点G.若∠1=36°,则∠2的大小是( )
如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF交CD于点G.若∠1=36°,则∠2的大小是( )| A. | 68° | B. | 70° | C. | 71° | D. | 72° |
17.甲、乙两班学生参加植树造林,已知甲班每天比乙班少植3棵树,甲班植60棵树与乙班植80棵树所用天数相等.若设甲班每天植树x棵,则可列方程( )
| A. | $\frac{60}{x}=\frac{80}{x+3}$ | B. | $\frac{60}{x}=\frac{80}{x-3}$ | C. | $\frac{60}{x-3}=\frac{80}{x}$ | D. | $\frac{60}{x+3}=\frac{80}{x}$ |
14. 若实数a,b在数轴上的位置如图所示,则以下说法正确的是( )
若实数a,b在数轴上的位置如图所示,则以下说法正确的是( )
 若实数a,b在数轴上的位置如图所示,则以下说法正确的是( )
若实数a,b在数轴上的位置如图所示,则以下说法正确的是( )| A. | a>b | B. | ab>0 | C. | a+b>0 | D. | |a|>|b| |
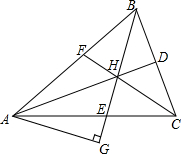 如图,在△ABC中,角平分线AD,BE,CF相交于点H,过A点作AG⊥BE,垂足为G,那么∠HAG=$\frac{1}{2}$∠ACB吗?为什么?
如图,在△ABC中,角平分线AD,BE,CF相交于点H,过A点作AG⊥BE,垂足为G,那么∠HAG=$\frac{1}{2}$∠ACB吗?为什么?
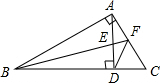 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D点,∠ABC的平分线分别交AD、AC于E、F两点,连结DF,下列结论:①△AEF为等腰三角形;②△FAD为等腰三角形;③△BDE∽△BAF;④△ABE∽△CBF,其中正确的有( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D点,∠ABC的平分线分别交AD、AC于E、F两点,连结DF,下列结论:①△AEF为等腰三角形;②△FAD为等腰三角形;③△BDE∽△BAF;④△ABE∽△CBF,其中正确的有( )