题目内容
3.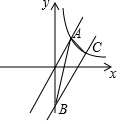 如图,已知直线y=kx与双曲线y=$\frac{4}{x}$(x>0)相交于点A(2,m),将直线y=kx向下平移2个单位长度后与y轴交于点B,与双曲线交于点C,连结AB,AC.
如图,已知直线y=kx与双曲线y=$\frac{4}{x}$(x>0)相交于点A(2,m),将直线y=kx向下平移2个单位长度后与y轴交于点B,与双曲线交于点C,连结AB,AC.(1)求直线BC的函数表达式;
(2)求△ABC的面积.
分析 (1)由点A在双曲线上求得点A的坐标,从而得出k=1,即可得出直线BC的解析式;
(2)过点A作AD∥y轴交BC于点D,先求得点D的坐标为(2,0),再求出点C的坐标,利用S△ABC=S△ABD+S△ACD可得答案.
解答 解:(1)∵点A在y=$\frac{4}{x}$的图象上,
∴m=2,
∴A(2,2),
∴k=1,
则直线BC的解析式为y=x-2;
(2)过点A作AD∥y轴交BC于点D,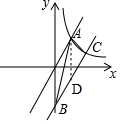
当x=2时,y=x-2=0,
∴D(2,0),
∴AD=2,
由$\left\{\begin{array}{l}{y=x-2}\\{y=\frac{4}{x}}\end{array}\right.$得x=1±$\sqrt{5}$,
∴点C(1+$\sqrt{5}$,$\sqrt{5}$-1),
∴S△ABC=S△ABD+S△ACD=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×(1+$\sqrt{5}$-2)=1+$\sqrt{5}$
点评 本题主要考查直线和双曲线的交点问题,熟练掌握待定系数法求函数解析式及割补法求三角形的面积是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.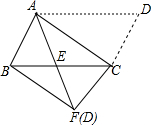 如图,将?ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )
如图,将?ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )
 如图,将?ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )
如图,将?ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图所示,已知一次函数y=2x+b的图象与x轴的交点坐标为(-2,0),则不等式2x+b>0的解集为x>-2.
如图所示,已知一次函数y=2x+b的图象与x轴的交点坐标为(-2,0),则不等式2x+b>0的解集为x>-2. 如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB.