题目内容
1．六（1）、（2）两个班共有24名女生和36名男生，活动时进行分组，如果将他们分成人数相等的若干个小组，而且每组男生和女生数相同，那么最多能分12 组．分析 根据题干可知：分组后每个小组的男生和女生人数分别相等，要求最多能分成几个组，那么这里只要求出24和36的最大公因数即可解决问题，两个数的公有质因数连乘积就是它们的最大公约数．
解答 解：24=2×2×2×3，36=2×2×3×3，
所以24和36的最大公因数是：2×2×3=12，
答：最多将他们分成12组．
故答案为：12．
点评 本题考查了有理数的乘法，利用求两个数的最大公因数的方法解决实际问题的方法的灵活应用．
练习册系列答案
相关题目
18．若二元一次方程组$\left\{\begin{array}{l}x+y=3\\ 3x-5y=4\end{array}\right.$的解为$\left\{\begin{array}{l}x=a\\ y=b\end{array}\right.$，则a-b=（ ）
| A． | 1 | B． | 3 | C． | $-\frac{1}{4}$ | D． | $\frac{7}{4}$ |
19．计算6m6÷（-2m2）3的结果为（ ）
| A． | -m | B． | -1 | C． | $\frac{3}{4}$ | D． | -$\frac{3}{4}$ |
16．
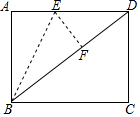如图，在矩形ABCD中BC=8，CD=6，将△ABE沿BE折叠，使点A恰好落在对角线BD上F处，则DE的长是（ ）
如图，在矩形ABCD中BC=8，CD=6，将△ABE沿BE折叠，使点A恰好落在对角线BD上F处，则DE的长是（ ）| A． | 3 | B． | $\frac{24}{5}$ | C． | 5 | D． | $\frac{89}{16}$ |
6．下列各题变形正确的是（ ）
| A． | 3（x+8）=3x+8 | B． | 6x+5=6（x+5） | C． | -（x-6）=x-6 | D． | -a+b=-（a-b） |
13．若某地打长途电话3分钟之内收费1.8元，3分钟以后每增加1分钟（不到1分钟按1分钟计算）加收0.5元，当通话时间t≥3分钟时，电话费y（元）与通话时间t（分）之间的关系式为y=0.5t+0.3．
10．下列图案，既是轴对称又是中心对称的是（ ）
| A． |  | B． |  | C． |  | D． |  |
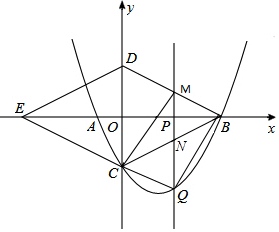如图，抛物线y=ax2+bx-4与x轴交于A（-2，0）、B（8，0）两点，与y轴交于点C，连接BC，以BC为一边，点O为对称中心做菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．