题目内容
18.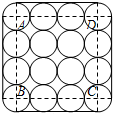 如图是一个组合烟花的横截面,其中16个圆的半径相同,点A、B、C、D分别是四个角上的圆的圆心,且四边形ABCD为正方形.若圆的半径为r,则组合烟花截面的周长和面积分别是多少?
如图是一个组合烟花的横截面,其中16个圆的半径相同,点A、B、C、D分别是四个角上的圆的圆心,且四边形ABCD为正方形.若圆的半径为r,则组合烟花截面的周长和面积分别是多少?
分析 根据图形可以看出截面的周长等于12个圆的直径和1个半径为r的圆的周长的和,截面的面积等于3个圆的直径长、4个圆的直径宽的长方形面积+3个圆的直径长、个圆的直径宽的长方形面积+1个圆面积.
解答 解:由图形知,正方形ABCD的边长为6r,
∴其周长为4×6r=24r,
∵一个圆的周长为:2πr,
∴截面的周长为:24r+2πr,
由图形得:截面的面积=3个圆的直径长、4个圆的直径宽的长方形面积+3个圆的直径长、个圆的直径宽的长方形面积+1个圆面积,
即截面的面积=6r×8r+6r×2r+πr2=(60+π)r2.
点评 本题考查了相切两圆的性质及圆面积、长方形面积的计算,熟练掌握图形的拆分变换是解决问题的关键.

练习册系列答案
相关题目
8.下列图形中,轴对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.如果x2-px+q=(x+a)(x+b),那么p等于( )
| A. | ab | B. | a+b | C. | -ab | D. | -(a+b) |
18.方程$\sqrt{x+1}$=5-x的解是( )
| A. | x=3 | B. | x=8 | C. | x1=3,x2=8 | D. | x1=3,x2=-8 |
 如图,A,B两处加工厂需从设在x轴上的C贷站和y轴上的D货站来回调运货物,当C,D建于何处时,AB+BC+CD+DA的路程最短?
如图,A,B两处加工厂需从设在x轴上的C贷站和y轴上的D货站来回调运货物,当C,D建于何处时,AB+BC+CD+DA的路程最短?