题目内容
12．先化简，再求值：（a-2b）2+（a+b）（a-b）-2（a-3b）（a-b），其中a=$\frac{1}{2}$，b=-3．分析 根据完全平方公式、平方差公式和多项式乘多项式可以化简题目中的式子，然后将a、b的值代入化简后的式子即可解答本题．
解答 解：（a-2b）2+（a+b）（a-b）-2（a-3b）（a-b）
=a2-4ab+4b2+a2-b2-2a2+8ab-6b2
=4ab-3b2，
当a=$\frac{1}{2}$，b=-3时，原式=4×$\frac{1}{2}×（-3）-3×（-3）^{2}$=-33．
点评 本题考查整式的混合运算-化简求值，解答此类问题的关键是明确整式的混合运算的计算方法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．计算（-3）3+52-（-2）2的值为（ ）
| A． | 2 | B． | -3 | C． | 5 | D． | -6 |
3．在直线AB上取一点O，过点O作射线OC，OD，使OC⊥OD，当∠AOC=30°时，∠BOD的度数（ ）
| A． | 60° | B． | 90° | C． | 120° | D． | 60°或120° |
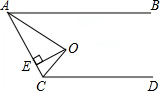如图，AB∥CD，O为∠BAC、∠ACD的平分线的交点，OE⊥AC于E，且OE=1，则AB与CD之间的距离等于2．
2．下列函数中，一次函数是（ ）
| A． | y=8x2 | B． | y=8x-1 | C． | y=x+1 | D． | y=$\frac{1}{x+1}$ |