题目内容
18．
如图，AB∥CD，E是CD上的一点，BE，CF交于点F．若∠B=45°，∠C=60°，则∠BFC=105°．
分析 先根据平行线的性质求出∠CEF的度数，再由三角形外角的性质即可得出结论．
解答 解：∵AB∥CD，∠B=45°，
∴∠CEF=∠B=45°．
∵∠BFC是△CEF的外角，∠C=60°，
∴∠BFC=∠CEF+∠C=45°+60°=105°．
故答案为：105°．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．
练习册系列答案
相关题目
17．-2的倒数是（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | -$\frac{1}{2}$ | D． | -2 |
9．下列平面图形中，既是轴对称图形，又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
6．若（a-2）2+（b+3）2=0，则（a+b）2015的值是（ ）
| A． | 0 | B． | 1 | C． | -l | D． | 2012 |
13．
如图，∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=1，则△A7B7A8的边长为（ ）
如图，∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=1，则△A7B7A8的边长为（ ）| A． | 6 | B． | 12 | C． | 32 | D． | 64 |
10．
如图，⊙O的直径CD⊥AB，∠CDB=25°，则∠AOC的度数为（ ）
如图，⊙O的直径CD⊥AB，∠CDB=25°，则∠AOC的度数为（ ）| A． | 25° | B． | 30° | C． | 40° | D． | 50° |
7．
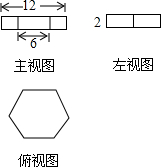如图所示是某几何体的三视图，则该几何体的体积是（ ）
如图所示是某几何体的三视图，则该几何体的体积是（ ）| A． | 18$\sqrt{3}$ | B． | 54$\sqrt{3}$ | C． | 108$\sqrt{3}$ | D． | 216$\sqrt{3}$ |
8．若x=-$\frac{1}{3}$，则|x|的值是（ ）
| A． | 3 | B． | -3 | C． | $\frac{1}{3}$ | D． | -$\frac{1}{3}$ |