题目内容
小明是一个既爱动手又爱动脑的学生,一次他将AB,CD两根木条平行钉在木板上,将一根橡皮筋固定在A,C两点,若点E是橡皮筋上一点,(如图1);

操作1:小明向右拽动E点将橡皮筋拉紧,出现∠A,∠C,∠AEC,(如图2);
发 现:图2中∠A,∠C,∠AEC之间的关系是 ;
操作2:小明试图改变AB,CD两木条平行为相交,且B与D两点重合(如图3);
计 算:图3中∠A=40°,∠C=15°,∠AEC=85°,AB,CDG两根木条相交而成的角∠ABC= 度:
操作3:小明试着在AB,CD两根平行木条之间的橡皮筋上增加F、G点,按如图4方向拽动E、F、G点将橡皮筋拉紧;
探 索:图4中又可以发现图中各角间的结论: .请试着说明理由.

操作1:小明向右拽动E点将橡皮筋拉紧,出现∠A,∠C,∠AEC,(如图2);
发 现:图2中∠A,∠C,∠AEC之间的关系是
操作2:小明试图改变AB,CD两木条平行为相交,且B与D两点重合(如图3);
计 算:图3中∠A=40°,∠C=15°,∠AEC=85°,AB,CDG两根木条相交而成的角∠ABC=
操作3:小明试着在AB,CD两根平行木条之间的橡皮筋上增加F、G点,按如图4方向拽动E、F、G点将橡皮筋拉紧;
探 索:图4中又可以发现图中各角间的结论:
考点:平行线的性质
专题:
分析:在图2中过E作EF∥AB,由平行线的性质可得∠A+∠C=∠AEC;在图3中,过E作射线BF,由三角形外角的性质可得到∠AEC=∠A+∠ABC+∠C,可求得答案;在图4中分别过E、F、G作AB的平行线,由平行线的性质可得到各角之间的关系.
解答:解:
在图2中,过E作EF∥AB,
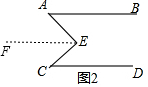
∵AB∥CD,
∴EF∥CD,
∴∠A=∠AEF,∠C=∠CEF,
∴∠AEC=∠AEF+∠CEF=∠A+∠C,
故发现的答案为:∠AEC=∠A+∠C;
在图3中,过E作射线BF,
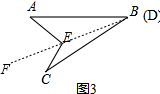
在△ABE中,∠AEF=∠A+∠ABF,
在△BCE中,∠CEF=∠C+∠CBF,
∴∠AEC=∠A+∠C+∠ABC,
∴∠ABC=∠AEC-∠A-∠C=85°-40°-15°=30°,
故计算的答案为:30;
在图4中,分别过E、F、G作AB的平行线EH、FI、GL,
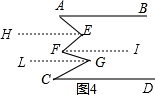
∵AB∥CD,
∴AB∥HE∥FI∥GL∥CD,
∴∠A=∠AEH,∠HEF=∠EFI,∠IFG=∠FGL,∠LGC=∠C,
∴∠A+∠EFG+∠C=∠AEF+∠FGC,
故探索的答案为:∠A+∠EFG+∠C=∠AEF+∠FGC.
在图2中,过E作EF∥AB,

∵AB∥CD,
∴EF∥CD,
∴∠A=∠AEF,∠C=∠CEF,
∴∠AEC=∠AEF+∠CEF=∠A+∠C,
故发现的答案为:∠AEC=∠A+∠C;
在图3中,过E作射线BF,

在△ABE中,∠AEF=∠A+∠ABF,
在△BCE中,∠CEF=∠C+∠CBF,
∴∠AEC=∠A+∠C+∠ABC,
∴∠ABC=∠AEC-∠A-∠C=85°-40°-15°=30°,
故计算的答案为:30;
在图4中,分别过E、F、G作AB的平行线EH、FI、GL,

∵AB∥CD,
∴AB∥HE∥FI∥GL∥CD,
∴∠A=∠AEH,∠HEF=∠EFI,∠IFG=∠FGL,∠LGC=∠C,
∴∠A+∠EFG+∠C=∠AEF+∠FGC,
故探索的答案为:∠A+∠EFG+∠C=∠AEF+∠FGC.
点评:本题主要考查平行线的性质和判定,掌握平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
甲乙两地相距150千米,一辆小汽车和一辆客车同时从两地相向开出,经过50分钟相遇,此时小汽车比客车多行驶30千米.设小汽车和客车的平均速度分别为x千米/小时和y千米/小时.则下列方程组正确的是( )
A、
| |||||||||||||
B、
| |||||||||||||
C、
| |||||||||||||
D、
|
 如图,下列推论及所注理由正确的是( )
如图,下列推论及所注理由正确的是( )| A、∵∠1=∠B,∴DE∥BC(两直线平行,同位角相等) |
| B、∵∠2=∠C,∴DE∥BC(两直线平行,同位角相等) |
| C、∵∠2+∠3+∠B=180°,∴DE∥BC(同旁内角互补,两直线平行) |
| D、∵∠4=∠1,∴DE∥BC(对顶角相等) |
当x≠-
时,
=2成立,则a2-b2等于( )
| 5 |
| b |
| a+x |
| -bx-5 |
| A、0 | B、1 |
| C、99.25 | D、99.75 |
 如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB=
如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB= 如图,∠B=40°,∠C=20°,∠CDB=3∠A,求∠A的度数.
如图,∠B=40°,∠C=20°,∠CDB=3∠A,求∠A的度数. 某工厂拟建一座平面图形为矩形且占地面积为200平方米的三级污水处理池,如图所示.由于地形限制,三级污水处理池的长、宽都不能超过16米,高h为2m.如果池的外围墙建造单价为每平方米400元,中间两条隔墙建造单价为每平方米300元(隔墙厚度不计),池底建造单价为每平方米80元(池墙的厚度忽略不计).求:当三级污水处理池的总造价为80000元时,池长x为多少?
某工厂拟建一座平面图形为矩形且占地面积为200平方米的三级污水处理池,如图所示.由于地形限制,三级污水处理池的长、宽都不能超过16米,高h为2m.如果池的外围墙建造单价为每平方米400元,中间两条隔墙建造单价为每平方米300元(隔墙厚度不计),池底建造单价为每平方米80元(池墙的厚度忽略不计).求:当三级污水处理池的总造价为80000元时,池长x为多少? 如图,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F,若CF⊥AD,AB=2,求DE的长.
如图,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F,若CF⊥AD,AB=2,求DE的长. 实数a,b在数轴上所对应的点的位置如图所示,化简|b-a|-
实数a,b在数轴上所对应的点的位置如图所示,化简|b-a|-