题目内容
已知a,b,c是△ABC三条边的长,那么方程cx2+(a+b)x+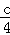 =0的根的情况是( )
=0的根的情况是( )
A.没有实数根 B.有两个不相等的正实数根
C.有两个不相等的负实数根 D.有两个异号实数根
C【考点】根与系数的关系;根的判别式;三角形三边关系.
【专题】压轴题.
【分析】判断上述方程的根的情况,只要看根的判别式△=b2﹣4ac的值的符号,结合三角形三边关系即可作出判断.
【解答】解:在此方程中△=b2﹣4ac=(a+b)2﹣4c×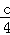 =(a+b)2﹣c2
=(a+b)2﹣c2
∵a,b,c是△ABC三条边的长
∴a>0,b>0,c>0.c<a+b,即(a+b)2>c2
∴△=(a+b)2﹣c2>0
故方程有两个不相等的实数根.
又∵两根的和是﹣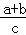 <0,两根的积是
<0,两根的积是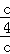 =
= >0
>0
∴方程有两个不等的负实根.
故选C
【点评】总结:一元二次方程根的情况与判别式△的关系:
(1)△>0⇔方程有两个不相等的实数根;
(2)△=0⇔方程有两个相等的实数根;
(3)△<0⇔方程没有实数根.
三角形三边关系:两边之和大于第三边,两边之差小于第三边.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,
| |
(1)请找出图2中与△ABE全等的三角形,并给予证明( 说明:结论中不得含
说明:结论中不得含
有未标识的字母);
 (2)求证:DC⊥BE.
(2)求证:DC⊥BE.
 -2(a-2).
-2(a-2). ,当函数值y随x的增大而减小时,x的取值范围是( )
,当函数值y随x的增大而减小时,x的取值范围是( ) )=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
)=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长. 化为一元二次方程的一般形式是__________,它的一次项系数是__________.
化为一元二次方程的一般形式是__________,它的一次项系数是__________. cm,请问蜗牛一共爬行了多少秒?
cm,请问蜗牛一共爬行了多少秒?