题目内容
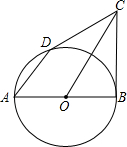AB是⊙O的直径，BC切⊙O于B．AD是弦．AD∥OC．OC交BC于C．求证：DC是⊙O的切线．考点：切线的判定
专题：证明题
分析：连接OD，要证明DC是⊙O的切线，只要证明∠ODC=90°即可．根据题意，可证△OCD≌△OCB，即可得∠CDO=∠CBO=90°，由此可证DC是⊙O的切线．
解答：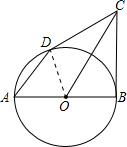
证明：连接OD；
∵OA=OD，
∴∠A=∠ADO．
∵AD∥OC，
∴∠A=∠BOC，∠ADO=∠COD．
∴∠BOC=∠COD．
在△OBC和△ODC中，
，
∴△OBC≌△ODC（SAS）．
∴∠OBC=∠ODC，
又∵BC是⊙O的切线．
∴∠OBC=90°．
∴∠ODC=90°．
∴DC是⊙O的切线．
证明：连接OD；∵OA=OD，
∴∠A=∠ADO．
∵AD∥OC，
∴∠A=∠BOC，∠ADO=∠COD．
∴∠BOC=∠COD．
在△OBC和△ODC中，
|
∴△OBC≌△ODC（SAS）．
∴∠OBC=∠ODC，
又∵BC是⊙O的切线．
∴∠OBC=90°．
∴∠ODC=90°．
∴DC是⊙O的切线．
点评：本题考查的是切线的判定及全等三角形的判定与性质．要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．
练习册系列答案
阅读快车系列答案
相关题目
火星和地球的距离约为340000000千米，用科学记数法表示340000000的结果是（ ）
| A、3.4×108千米 |
| B、3.4×105千米 |
| C、34×104 |
| D、3.4×104 |
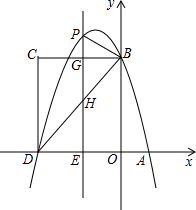如图，在平面直角坐标系中，抛物线y=-x2+bx+c与x轴交于A、D两点，与y轴交于点B，四边形OBCD是正方形．点B坐标为（0，4），已知点E（m，0）是线段DO上的动点（m＜0），过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．