题目内容
甲、乙两单位为爱心基金捐款,其中甲单位捐款9600元,乙单位捐款12000元,已知乙单位捐款人数比甲单位多50人,且两单位人均捐款数相等.问这两单位共有多少人捐款?人均捐款额是多少?
考点:分式方程的应用
专题:
分析:设甲单位有x人捐款,乙单位有(x+50)人捐款,根据两单位人均捐款数相等.列方程求解.
解答:解:设甲单位有x人捐款,乙单位有(x+50)人捐款,
由题意得,
=
,
解得:x=200,
经检验,x=200是原分式方程的解,且符合题意,
则乙单位的捐款人数为200+50=250,
总捐款人数为:250+200=450(人),
人均捐款数为:
=48(元).
答:这两单位共有450人捐款,人均捐款额为48元.
由题意得,
| 9600 |
| x |
| 12000 |
| x+50 |
解得:x=200,
经检验,x=200是原分式方程的解,且符合题意,
则乙单位的捐款人数为200+50=250,
总捐款人数为:250+200=450(人),
人均捐款数为:
| 9600 |
| 200 |
答:这两单位共有450人捐款,人均捐款额为48元.
点评:本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解.

练习册系列答案
相关题目
 观察图中的函数图象,得关于x的不等式ax<bx+c的解集为( )
观察图中的函数图象,得关于x的不等式ax<bx+c的解集为( )| A、x<3 | B、x<1 |
| C、x<0 | D、x>1 |
计算
(1)-43÷5×
(2)-1.53×0.75+0.53×
-3.4×0.75
(3)-(1-0.5)÷
×[2+(-4)2]
(4)[-
-(-1
)+2
]×(-48)-(-1)3.
(1)-43÷5×
| 1 |
| 5 |
(2)-1.53×0.75+0.53×
| 3 |
| 4 |
(3)-(1-0.5)÷
| 1 |
| 3 |
(4)[-
| 5 |
| 12 |
| 1 |
| 2 |
| 1 |
| 6 |
 如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D同时以同样的速度沿边BC,DC向点C运动.给出以下四个结论:①AE=AF;②∠CEF=∠CFE;③当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;④当点E,F分别为边BC,DC的中点时,△AEF的面积最大.正确的是( )
如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D同时以同样的速度沿边BC,DC向点C运动.给出以下四个结论:①AE=AF;②∠CEF=∠CFE;③当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;④当点E,F分别为边BC,DC的中点时,△AEF的面积最大.正确的是( ) 如图,△ABC中 AE交BC于点D,AD=4,DE=2.4,BE=6,BD:DC=5:3,则AC的长等于多少.
如图,△ABC中 AE交BC于点D,AD=4,DE=2.4,BE=6,BD:DC=5:3,则AC的长等于多少.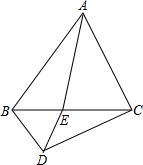 如图,△ABC是等边三角形,E为BC边上一点,将三角形ABE绕点B按顺时针方向旋转后,能与△CBD重合.若BE=3cm,则DE=
如图,△ABC是等边三角形,E为BC边上一点,将三角形ABE绕点B按顺时针方向旋转后,能与△CBD重合.若BE=3cm,则DE=