题目内容
 如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F. 请解答下列问题:
如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F. 请解答下列问题:(1)连结BD,试说明∠BDE=∠CDF;
(2)求证:BE=FC;
(2)若AE=4,FC=3,求EF长.
考点:全等三角形的判定与性质,等腰三角形的性质,勾股定理
专题:
分析:(1)因为DE⊥DF,所以∠EDF=∠BDC=90°,所以∠BDE+∠BDF=∠BDF+∠CDF,即∠BDE=∠CDF;
(2)由等腰三角形“三线合一”得∠EBD=∠DBC=
∠ABC=45°=∠C,再通过证明△DEB≌△DFC,即可得到BE=FC;
(3)在Rt△EBF中,利用勾股定理即可求出EF的长.
(2)由等腰三角形“三线合一”得∠EBD=∠DBC=
| 1 |
| 2 |
(3)在Rt△EBF中,利用勾股定理即可求出EF的长.
解答:解:(1)∵等腰三角形ABC中,∠ABC=90°
∴AB=BC,∠A=∠C=45°,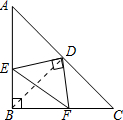
∵D是AC边上中点,
∴BD⊥AC,
又∵DE⊥DF,
∴∠EDF=∠BDC=90°,
∴∠BDE+∠BDF=∠BDF+∠CDF,
即∠BDE=∠CDF;
(2)由等腰三角形“三线合一”得∠EBD=∠DBC=
∠ABC=45°=∠C,
∴DB=DC,
在△DEB和△DFC中,
,
∴△DEB≌△DFC(ASA),
∴EB=FC;
(3)EB=FC=3,AB=BC=7,BF=BC-FC=4,
在Rt△EBF中,∠B=90°,EF=
=
=5.
∴AB=BC,∠A=∠C=45°,

∵D是AC边上中点,
∴BD⊥AC,
又∵DE⊥DF,
∴∠EDF=∠BDC=90°,
∴∠BDE+∠BDF=∠BDF+∠CDF,
即∠BDE=∠CDF;
(2)由等腰三角形“三线合一”得∠EBD=∠DBC=
| 1 |
| 2 |
∴DB=DC,
在△DEB和△DFC中,
|
∴△DEB≌△DFC(ASA),
∴EB=FC;
(3)EB=FC=3,AB=BC=7,BF=BC-FC=4,
在Rt△EBF中,∠B=90°,EF=
| EB2+BF2 |
| 32+42 |
点评:此题主要考查学生对全等三角形的判定与性质和等腰直角三角形的理解和掌握和勾股定理的运用,稍微有点难度,属于中档题

练习册系列答案
相关题目
 如图,C为BE上一点,以BC、CE为边向线段BE同侧作等边△ABC、等边△CDE,BD交AC于M,交AE于点G,AE交CD于N,连接CG.
如图,C为BE上一点,以BC、CE为边向线段BE同侧作等边△ABC、等边△CDE,BD交AC于M,交AE于点G,AE交CD于N,连接CG. 如图,直线AB与CD相交于O,OF、OD分别是∠AOE、∠BOE的平分线.
如图,直线AB与CD相交于O,OF、OD分别是∠AOE、∠BOE的平分线. 如图,已知线段AB=26,BC=18,点M是AC的中点.
如图,已知线段AB=26,BC=18,点M是AC的中点. 已知直线l上有一点O,点A、B同时从O出发,在直线l上分别向左、向右作匀速运动,且A、B的速度比为1:2,设运动时间为ts.
已知直线l上有一点O,点A、B同时从O出发,在直线l上分别向左、向右作匀速运动,且A、B的速度比为1:2,设运动时间为ts. 如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连结BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连结BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E. 如图,在数轴上点A、O、C、B表示的数分别是a,0,1,b,且O为线段AB的中点.那么|a+b|+|
如图,在数轴上点A、O、C、B表示的数分别是a,0,1,b,且O为线段AB的中点.那么|a+b|+|