题目内容
17.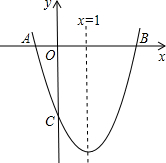 如图,已知抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A、B两点,交y轴于C点,其中A点的坐标为(-1,0).
如图,已知抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A、B两点,交y轴于C点,其中A点的坐标为(-1,0).(1)写出点B、点C的坐标;
(2)求抛物线y=ax2+bx-3的顶点.
分析 (1)将x=0代入可求得y=-3,从而得到点C的坐标,由抛物线的对称性可求得点B的坐标;
(2)将点A、B的坐标代入得到关于a、b的方程组,从而可求得a、b的值,从而得到函数的解析式,最后将x=1,可求得y=-4,从而可求得抛物线的顶点坐标.
解答 解:(1)∵将x=0代入得:y=-3.
∴点C的坐标为(0,-3).
∵点A与点B关于x=1对称,
∴点B的坐标为(3,0).
(2)将(-1,0)、(3,0)代入得:$\left\{\begin{array}{l}{a-b-3=0}\\{9a+3b-3=0}\end{array}\right.$,
解得:a=1,b=-2.
∴抛物线的解析式为y=x2-2x-3.
将x=1代入得:y=-4.
∴抛物线的顶点坐标为(1,-4).
点评 本题主要考查的是二次函数的图象和性质,利用抛物线的对称性求得点B的坐标是解题关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
7.下列各组中代表的三条线段(a≠0)能组成三角形( )
| A. | 3a2,4a2,8a2 | B. | 5a2,6a2,11a2 | C. | 5a2,6a2,10a2 | D. | 4a2,4a2,8a2 |
8.关于x的方程ax2+4x-1=0有实数根,则a的取值范围是( )
| A. | a≤-4 | B. | a≥-4 | C. | a≤-4且a≠0 | D. | a≥-4且a≠0 |
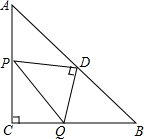 如图,等腰Rt△ABC中,∠C=90°,AC=BC,D是AB的中点,P是线段AC上的动点,连接PD,作DQ⊥PD交线段CB于Q,连接PQ,则点P从A向C方向运动过程中,△CPQ的面积变化是先逐渐增大,再逐渐减小.
如图,等腰Rt△ABC中,∠C=90°,AC=BC,D是AB的中点,P是线段AC上的动点,连接PD,作DQ⊥PD交线段CB于Q,连接PQ,则点P从A向C方向运动过程中,△CPQ的面积变化是先逐渐增大,再逐渐减小. 一次函数y=-$\frac{3}{2}$x+3的图象如图所示,则不等式-$\frac{3}{2}$x+3>-3的解是x<4.
一次函数y=-$\frac{3}{2}$x+3的图象如图所示,则不等式-$\frac{3}{2}$x+3>-3的解是x<4.