题目内容
7.己知点($\frac{6}{p}$,$\frac{p}{2}$)在函数y=$\frac{k}{x}$(x>0)的图象上,A,B为该函数图象上两点,联结AB并延长交y轴于C,过A作AD垂直y轴于D,已知AB=CB,且点B的横坐标为m.(1)求点C的纵坐标(用含m的代数式表示);
(2)联结BD,若∠ADB=45°,求m.
分析 (1)作BE⊥y轴于E,根据反比例函数图象上点的特征求出k的值,根据题意求出A、B的坐标,运用待定系数法求出直线AB的解析式,得到点C的纵坐标;
(2)作BF⊥DA于F,根据直角三角形的性质列出方程,解方程即可.
解答 解:(1)作BE⊥y轴于E,
∵点($\frac{6}{p}$,$\frac{p}{2}$)在函数y=$\frac{k}{x}$(x>0)的图象上,
∴k=$\frac{6}{p}$×$\frac{p}{2}$=3,
∵BE∥AD,AB=CB,
∴AD=2BE,点B的横坐标为m.
∴点D的横坐标为2m,
则点B的纵坐标为$\frac{3}{m}$,点A的纵坐标为$\frac{3}{2m}$.
∴点B的坐标为(m,$\frac{3}{m}$),点A的坐标为(2m,$\frac{3}{2m}$),
设直线AB的解析式为:y=kx+b,
$\left\{\begin{array}{l}{mk+b=\frac{3}{m}}\\{2mk+b=\frac{3}{2m}}\end{array}\right.$,
解得,k=-$\frac{3}{2m}$,b=$\frac{9}{2m}$,
∴点C的纵坐标为$\frac{9}{2m}$;
(2) 作BF⊥DA于F,
作BF⊥DA于F,
∵∠ADB=45°,BF⊥DA,
∴DF=BF,
即$\frac{3}{m}$-$\frac{3}{2m}$=m,
解得,m1=$\frac{\sqrt{6}}{2}$,m2=-$\frac{\sqrt{6}}{2}$(舍去),
∴m=$\frac{\sqrt{6}}{2}$.
点评 本题考查的是反比例函数的性质、坐标与图形的关系,待定系数法求一次函数解析式以及三角形中位线定理,灵活运用相关的性质定理、正确作出辅助线是解题的关键.

| A. | 一般四边形 | B. | 平行四边形 | C. | 正方形 | D. | 长方形 |
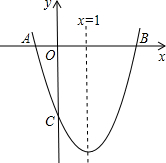 如图,已知抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A、B两点,交y轴于C点,其中A点的坐标为(-1,0).
如图,已知抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A、B两点,交y轴于C点,其中A点的坐标为(-1,0).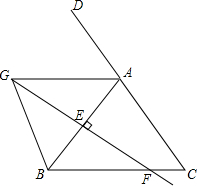 已知,如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB、BC于E、F,∠BAD的平分线交直线EF于G,求证:BG=BF.
已知,如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB、BC于E、F,∠BAD的平分线交直线EF于G,求证:BG=BF.