题目内容
8．关于x的方程ax2+4x-1=0有实数根，则a的取值范围是（ ）| A． | a≤-4 | B． | a≥-4 | C． | a≤-4且a≠0 | D． | a≥-4且a≠0 |
分析 分a=0和a≠0两种情况进行讨论，据此求出a的取值范围．
解答 解：当a=0时，4x-1=0，方程有解；
当a≠0时，ax2+4x-1=0有实数根，
则△=16+4a≥0，
解得a≥-4，
综上a≥-4．
故选B．
点评 本题主要考查了根的判别式以及一元一次方程的解的知识，解答本题的关键是掌握根的判别式与方程根的个数关系，此题难度不大．
练习册系列答案
相关题目
5．
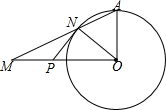如图，△AOM中，OA⊥OM，OA=2，以O为圆心，OA为半径作⊙O交AM于N，过点N作⊙O的切线交OM于P，若PM、PN为关于x的一元二次方程x2+（m-2）x+m+1=0的两根，求S△AOM．
如图，△AOM中，OA⊥OM，OA=2，以O为圆心，OA为半径作⊙O交AM于N，过点N作⊙O的切线交OM于P，若PM、PN为关于x的一元二次方程x2+（m-2）x+m+1=0的两根，求S△AOM．
3．在算式am+n÷□=am+2中，□内的代数式应是（ ）
| A． | am+n+2 | B． | an-2 | C． | am+n-2 | D． | an+2 |
13．下列比较大小错误的是（ ）
| A． | -0.02＜1 | B． | $\frac{4}{5}$＞$\frac{3}{4}$ | C． | -（-$\frac{3}{4}$）＞-|-0.75| | D． | -$\frac{22}{7}$＞-3.14 |
20．已知x+y=10，xy=24，则x2+y2的值为（ ）
| A． | 52 | B． | 148 | C． | 58 | D． | 76 |
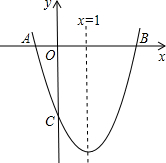如图，已知抛物线y=ax2+bx-3的对称轴为直线x=1，交x轴于A、B两点，交y轴于C点，其中A点的坐标为（-1，0）．