题目内容
18.关于x的方程mx2+x-m+1=0,有以下三个结论:①当m=0时,方程只有一个实数解;②当m≠0时,方程有两个不等的实数解;③无论m取何值,方程都有一个负数解,其中正确的是①③(填序号).分析 分别讨论m=0和m≠0时方程mx2+x-m+1=0根的情况,进而填空.
解答 解:当m=0时,x=-1,方程只有一个解,①正确;
当m≠0时,方程mx2+x-m+1=0是一元二次方程,△=1-4m(1-m)=1-4m+4m2=(2m-1)2≥0,方程有两个实数解,②错误;
把mx2+x-m+1=0分解为(x+1)(mx-m+1)=0,
当x=-1时,m-1-m+1=0,即x=-1是方程mx2+x-m+1=0的根,③正确;
故答案为①③.
点评 本题主要考查了根的判别式以及一元一次方程的解的知识,解答本题的关键是掌握根的判别式的意义以及分类讨论的思想.

练习册系列答案
相关题目
8.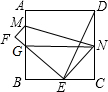 如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )
如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )
 如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )
如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
9.为庆祝抗战胜利70周年,我市某楼盘让利于民,决定将原价为a元/米2的商品房价降价10%销售,降价后的销售价为( )
| A. | a-10% | B. | a•10% | C. | a(1-10%) | D. | a(1+10%) |
13.设二次函数y=(x-3)2-4图象的对称轴为直线l,若点M在直线l上,则点M的坐标可能是( )
| A. | (1,0) | B. | (3,0) | C. | (-3,0) | D. | (0,-4) |
3.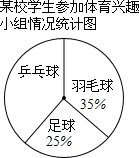 某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )
某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )
 某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )
某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )| A. | 25人 | B. | 35人 | C. | 40人 | D. | 100人 |
8.化简$\sqrt{12}$的结果是( )
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{6}$ |
 解不等式组:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$,并把解集在数轴上表示出来.