题目内容
7.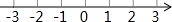 解不等式组:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$,并把解集在数轴上表示出来.
分析 先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{4x>2x-6①}\\{\frac{x-1}{3}≤\frac{x+1}{9}②}\end{array}\right.$
∵解不等式①得:x>-3,
解不等式②得:x≤2,
∴不等式组的解集为-3<x≤2,
在数轴上表示不等式组的解集为: .
.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集的应用,解此题的关键是能根据不等式的解集求出不等式组的解集,难度适中.

练习册系列答案
相关题目
15.如果一个正多边形的中心角为72°,那么这个多边形的边数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
12.下列计算正确的是( )
| A. | a2+a2=a4 | B. | a2•a3=a6 | C. | (-a2)2=a4 | D. | (a+1)2=a2+1 |
16.已知⊙O的半径为5,直线l是⊙O的切线,则点O到直线l的距离是( )
| A. | 2.5 | B. | 3 | C. | 5 | D. | 10 |
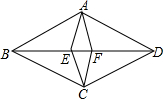 如图,四边形ABCD与四边形AECF都是菱形,点E、F在BD上.已知∠BAD=120°,∠EAF=30°,则$\frac{AB}{AE}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
如图,四边形ABCD与四边形AECF都是菱形,点E、F在BD上.已知∠BAD=120°,∠EAF=30°,则$\frac{AB}{AE}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$. 如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为3.
如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为3.