��Ŀ����
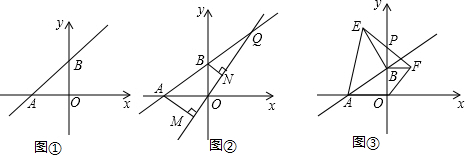
10����ͼ����ʾ��ֱ��L��y=m��x+10����x�Ḻ���ᡢy��������ֱ���A��B���㣮��1����OA=OBʱ����ȷ��ֱ��L�Ľ���ʽ��
��2���ڣ�1���������£���ͼ����ʾ����QΪAB�ӳ�����һ�㣬��ֱ��OQ����A��B����ֱ���AM��OQ��M��BN��OQ��N����AM=8��BN=6����MN�ij���
��3����mȡ��ͬ��ֵʱ����B��y�����������˶����ֱ���OB��ABΪ�ߣ���BΪֱ�Ƕ����ڵ�һ����������������ֱ�ǡ�OBF�͵���ֱ�ǡ�ABE����EF��y����P�㣬��ͼ�ۣ�
�ʣ�����B��y�����������˶�ʱ���Բ���PB�ij��Ƿ�Ϊ��ֵ�����ǣ��������ֵ�������ǣ�˵�����ɣ�
���� ��1����y=0�����x=-10���Ӷ�����õ�A�����꣬��x=0��y=10m����OA=OB��֪��B��������Ϊ10���Ӷ������m��ֵ��
��2������AAS֤����AMO�ա�ONB����ȫ�������ε����ʿ�֪ON=AM��OM=BN�������MN=AM+BN�����MN�ij���
��3������E��EG��y����G�㣬��֤����ABO�ա�EGB���Ӷ��õ�BG=10��Ȼ��֤����BFP�ա�GEP���Ӷ��õ�BP=GP=$\frac{1}{2}$BG��
��� �⣺��1��������֪��A��-10��0����B��0��10m��
��OA=OB��
��10m=10����m=1��
��L�Ľ���ʽy=x+10��
��2����AM��OQ��BN��OQ
���AMO=��BNO=90��
���AOM+��MAO=90��
�ߡ�AOM+BON=90��
���MAO=��NOB
�ڡ�AMO�͡�ONB�У�
$\left\{\begin{array}{l}{��AMO=��BNO}\\{��MAO=��NOB}\\{OA=OB}\end{array}\right.$��
���AMO�ա�ONB��
��ON=AM��OM=BN��
��AM=8��BN=6��
��MN=AM+BN=14��
��3��PB�ij�Ϊ��ֵ��
���ɣ���ͼ��ʾ������E��EG��y����G�㣮
�ߡ�AEBΪ����ֱ�������Σ�
��AB=EB����ABO+��EBG=90�㣮
��EG��BG��
���GEB+��EBG=90�㣮
���ABO=��GEB��
�ڡ�ABO�͡�EGB�У�
$\left\{\begin{array}{l}{��EGB=��BOA}\\{��ABO=��GEB}\\{AB=EB}\end{array}\right.$��
���ABO�ա�EGB��
��BG=AO=10��OB=EG
�ߡ�OBFΪ����ֱ�������Σ�
��OB=BF
��BF=EG��
�ڡ�BFP�͡�GEP�У�
$\left\{\begin{array}{l}{��EGP=��FBP}\\{��EPG=��FPB}\\{EG=BF}\end{array}\right.$��
���BFP�ա�GEP��
��BP=GP=$\frac{1}{2}$BG=5��
���� ������Ҫ�������һ�κ������ۺ�Ӧ�ã��������ҪӦ����һ�κ���ͼ���ϵ�����������ʽ�Ĺ�ϵ��ȫ�������ε����ʺ��ж�������ֱ�������ε����ʣ���������ȫ�������ε��ж������ǽ���Ĺؼ���

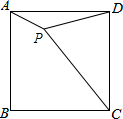 ��ͼ����������ABCD����һ��P��PA=1��PD=2��PC=3�����APD�Ķ���Ϊ��������
��ͼ����������ABCD����һ��P��PA=1��PD=2��PC=3�����APD�Ķ���Ϊ��������| A�� | 100�� | B�� | 120�� | C�� | 135�� | D�� | 150�� |
| A�� | a2•a4=a8 | B�� | $\sqrt{4}$=��2 | C�� | $\frac{-x-y}{x-y}$=-1 | D�� | a4��a2=a2 |
| A�� | �߶� | B�� | ���������� | C�� | �ı��� | D�� | Բ |
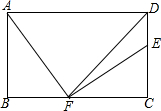 ��ͼ���ھ���ABCD�У�AD=12��AB=7��DFƽ�֡�ADC��AF��EF��
��ͼ���ھ���ABCD�У�AD=12��AB=7��DFƽ�֡�ADC��AF��EF��