题目内容
3. 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(2,-1)、B(4,3);
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(0,0)、B′(2,4)、C′(-1,3);
(3)画出移动后的图形.
(4)求△A′B′C′的面积.
分析 (1)直接利已知图形得出对应点坐标;
(2)利用平移的性质得出对应点坐标即可;
(3)利用(2)中各点坐标得出图形即可;
(4)利用△A′B′C′所在矩形面积减去周围三角形面积进而得出答案.
解答  解:(1)如图所示:A(2,-1),B(4,3);
解:(1)如图所示:A(2,-1),B(4,3);
(2)如图所示:A′(0,0),B′(2,4),C′(-1,3);
故答案为:(0,0),(2,4),(-1,3);
(3)如图所示:△A′B′C′即为所求;
(4)△A′B′C′的面积为:3×4-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×4=5.
点评 此题主要考查了平移变换以及三角形面积求法,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
13.随着天气变热,很多学生都想去游泳,但是野外游泳非常危险,并且很不卫生,我国每年大约有5万青少年或儿童死于溺水,在非正常死亡中占较大比例,因此,我们一定不要私自在野外游泳,最理想的地方是游泳馆.有一家游泳馆的收费为30元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A 类 | 50 | 25 |
| B 类 | 200 | 20 |
| C 类 | 400 | 15 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
8.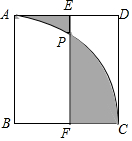 如图,在边长为2的正方形ABCD中,以B点为圆心,AB为半径构造扇形ABC,点P是AC上一动点,过P作EF⊥BC,分别交AD、BC于E、F.记AE、PE、$\widehat{AP}$构成的封闭区域为S1,PF、FC、$\widehat{PC}$构成的封闭区域为S2,当S1与S2面积相等时,BF的长为( )
如图,在边长为2的正方形ABCD中,以B点为圆心,AB为半径构造扇形ABC,点P是AC上一动点,过P作EF⊥BC,分别交AD、BC于E、F.记AE、PE、$\widehat{AP}$构成的封闭区域为S1,PF、FC、$\widehat{PC}$构成的封闭区域为S2,当S1与S2面积相等时,BF的长为( )
 如图,在边长为2的正方形ABCD中,以B点为圆心,AB为半径构造扇形ABC,点P是AC上一动点,过P作EF⊥BC,分别交AD、BC于E、F.记AE、PE、$\widehat{AP}$构成的封闭区域为S1,PF、FC、$\widehat{PC}$构成的封闭区域为S2,当S1与S2面积相等时,BF的长为( )
如图,在边长为2的正方形ABCD中,以B点为圆心,AB为半径构造扇形ABC,点P是AC上一动点,过P作EF⊥BC,分别交AD、BC于E、F.记AE、PE、$\widehat{AP}$构成的封闭区域为S1,PF、FC、$\widehat{PC}$构成的封闭区域为S2,当S1与S2面积相等时,BF的长为( )| A. | 1 | B. | $\frac{4}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{π}{2}$ |
 如图,在⊙O中,$\widehat{AC}$=$\widehat{BC}$,OD=$\frac{1}{2}$AO,OE=$\frac{1}{2}$OB,求证:CD=CE.
如图,在⊙O中,$\widehat{AC}$=$\widehat{BC}$,OD=$\frac{1}{2}$AO,OE=$\frac{1}{2}$OB,求证:CD=CE.