Question

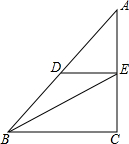
12．完成求解过程，并写出括号里的理由：
如图，在直角△ABC中，∠C=90°，DE∥BC，BE平分∠ABC，∠ADE=40°，求∠BEC的度数．
解：∵DE∥BC（已知）
∴∠ABC=∠ADE=40°两直线平行，同位角相等
∵BE平分∠ABC（已知）
∴∠CBE=$\frac{1}{2}$=20度
∵在Rt△ABC中，∠C=90°（已知）
∴∠BEC=90°-∠CBE=70度．

Answer 1

分析 由平行线的性质得出同位角相等∠ABC=∠ADE=40°，由角平分线的定义得出∠CBE=$\frac{1}{2}$∠ABC=20°，再由直角三角形的两个锐角互余即可得出结果．

解答 解：∵DE∥BC（已知）
∴∠ABC=∠ADE=40°（ 两直线平行，同位角相等  ）
∵BE平分∠ABC（已知）
∴∠CBE=$\frac{1}{2}$∠ABC=20°，
∵在Rt△ABC中，∠C=90°（已知）
∴∠BEC=90°-∠CBE=70°（ 直角三角形的两个锐角互余 ）．
故答案为：∠ABC，两直线平行，同位角相等；20，70．

点评 本题考查了平行线的性质、角平分线的定义、直角三角形的性质；熟练掌握平行线的性质，弄清角之间的数量关系是解决问题的关键．