Question

当b=________时，抛物线y=4x²-8x+4在直线y=x+b上截得的弦长等于2．

Answer 1

分析：设抛物线与直线交点为A（x₁，y₁），B（x₂，y₂），根据平面坐标系中两点间的距离公式得（x₁-x₂）²+（y₁-y₂）²=AB²=4，联立直线与抛物线的解析式可得x₁，x₂是方程4x²-8x+4=x+b即4x²-9x+（4-b）=0的二根，再利用两根关系解方程即可．
解答：设抛物线与直线交点为A（x₁，y₁），B（x₂，y₂）
则y₁=x₁+b，y₂=x₂+b，
∵AB=2，
∴（x₁-x₂）²+（y₁-y₂）²=4，
即2（x₁-x₂）²=4，（x₁+x₂）²-4x₁x₂=2，
又x₁，x₂是方程4x²-8x+4=x+b即4x²-9x+（4-b）=0的二根，
∴△=（-9）²-16（4-b）≥0，解得b≥-，
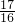x₁+x₂=，x₁x₂=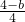，代入（x₁+x₂）²-4x₁x₂=2中，得
-4•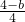=2，解得b=．
故本题答案为：．
点评：本题考查了二次函数与一次函数的交点坐标的求法，两点间距离公式的运用，根与系数关系的运用，具有较强的综合性．