题目内容
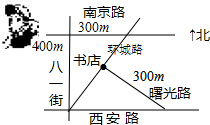 如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )| A、500m | B、525m |
| C、575m | D、625m |
考点:勾股定理的应用
专题:
分析:由于BC∥AD,那么有∠DAE=∠ACB,由题意可知∠ABC=∠DEA=90°,BA=ED,利用AAS可证△ABC≌△DEA,于是AE=BC=300,再利用勾股定理可求AC,即可求CE,根据图可知从B到E的走法有两种,分别计算比较即可.
解答: 解:如右图所示,
解:如右图所示,
∴∠DAE=∠ACB,
又∵BC⊥AB,DE⊥AC,
∴∠ABC=∠DEA=90°,
又∵AB=DE=400m,
∴△ABC≌△DEA,
∴EA=BC=300m,
在Rt△ABC中,AC=
=500m,
∴CE=AC-AE=200,
从B到E有两种走法:①BA+AE=700m;②BC+CE=500m,
∴最近的路程是500m.
故选A.
 解:如右图所示,
解:如右图所示,∴∠DAE=∠ACB,
又∵BC⊥AB,DE⊥AC,
∴∠ABC=∠DEA=90°,
又∵AB=DE=400m,
∴△ABC≌△DEA,
∴EA=BC=300m,
在Rt△ABC中,AC=
| AB2+BC2 |
∴CE=AC-AE=200,
从B到E有两种走法:①BA+AE=700m;②BC+CE=500m,
∴最近的路程是500m.
故选A.
点评:本题考查了平行线的性质、全等三角形的判定和性质、勾股定理.解题的关键是证明△ABC≌△DEA,并能比较从B到E有两种走法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
顺次连接四边形四边中点所组成的四边形是矩形,则原四边形为( )
| A、平行四边形 |
| B、对角线垂直的四边形 |
| C、对角线相等的四边形 |
| D、直角梯形 |
220名学生参加百分制的考试(得分以整数计),没有三名以上的学生得分相同,则恰有三名学生得分相同的个数的最小值是( )
| A、17 | B、18 | C、19 | D、20 |
考察50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组的数据个数分别是2,8,15,5,则第四组的频率是( )
| A、20 | B、0.4 |
| C、0.6 | D、30 |
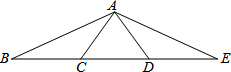 如图,若∠BAC=37°,且AC=BC=AD=DE,则∠BAE=
如图,若∠BAC=37°,且AC=BC=AD=DE,则∠BAE=