题目内容
已知一元二次方程两根之差为p，积为q，二次项系数为1，则该方程是 ．
考点：根与系数的关系
专题：
分析：先设一元二次方程两根为x1和x2，再求出x1+x2，最后根据二次项系数为1，即可得出答案．
解答：解：设一元二次方程两根为x1和x2，
则x1-x2=p，x1x2=q，
则（x1+x2）2=（x1-x2）2+4x1x2=p2-4q，
x1+x2=±
，
∵二次项系数为1，
∴该方程是x2+
x+q=0或x2-
x+q=0，
故答案为：x2+
x+q=0或x2-
x+q=0．
则x1-x2=p，x1x2=q，
则（x1+x2）2=（x1-x2）2+4x1x2=p2-4q，
x1+x2=±
| p2-4q |
∵二次项系数为1，
∴该方程是x2+
| p2-4q |
| p2-4q |
故答案为：x2+
| p2-4q |
| p2-4q |
点评：此题主要考查了根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法．
练习册系列答案
53天天练系列答案
相关题目
四边形ABCD中∠DAB=60°，∠B=∠D=Rt∠，BC=1，CD=2．余姚某校为了了解学生在校午餐所需的时间，抽量了20名学生在校午餐所需时间，获得如下的数据（单位：分）：10、12、15、8、16、18、19、18、20、18、18、20、28、22、25、20、15、16、21、16．若将这些数据以4分为组距进行分组，则组数是（ ）
| A、4组 | B、5组 | C、6组 | D、7组 |
下列说法正确的是（ ）
| A、在同一平面内，过已知直线外一点作这条直线的垂线有且只有一条 |
| B、连结直线外一点和直线上任一点，使这条线段垂直于已知直线 |
| C、作出点P到直线的距离 |
| D、连结直线外一点和直线上任一点的线段长是点到直线的距离 |
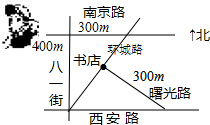如图，西安路与南京路平行，并且与八一街垂直，曙光路与环城路垂直．如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程约为（ ）| A、500m | B、525m |
| C、575m | D、625m |
如图，四边形ABCD是菱形，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F，连接CE．