题目内容
已知函数y=
,则使y=k成立的x值恰好有三个,则k的值为( )
|
| A、0 | B、1 | C、2 | D、3 |
考点:二次函数的性质
专题:计算题
分析:大致画出两抛物线,注意取值范围,可得到它们的交点为(3,3),所以直线y=3与两抛物线有三个交点,则得到k=3.
解答: 解:如图,
解:如图,
当y=k成立的x值恰好有三个,即直线y=k与两抛物线有三个交点,
而当x=3,两函数的函数值都为3,即它们的交点为(3,3),
所以k=3.
故选D.
 解:如图,
解:如图,当y=k成立的x值恰好有三个,即直线y=k与两抛物线有三个交点,
而当x=3,两函数的函数值都为3,即它们的交点为(3,3),
所以k=3.
故选D.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-b2a,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A、在同一平面内,过已知直线外一点作这条直线的垂线有且只有一条 |
| B、连结直线外一点和直线上任一点,使这条线段垂直于已知直线 |
| C、作出点P到直线的距离 |
| D、连结直线外一点和直线上任一点的线段长是点到直线的距离 |
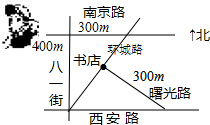 如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )| A、500m | B、525m |
| C、575m | D、625m |
下列运算正确的是( )
| A、(-x-y)2=x2+2xy+y2 |
| B、(-a-b) (a+b)=a2-b2 |
| C、(m-3)(m+2)=m2-6 |
| D、(a-b)2=a2-b2 |
 如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.
如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE. 如图,矩形ABCD的两边AB=3,BC=4,P是AD上任一点,PE⊥AC于点E,PF⊥BD于点F.求PE+PF的值.
如图,矩形ABCD的两边AB=3,BC=4,P是AD上任一点,PE⊥AC于点E,PF⊥BD于点F.求PE+PF的值.