题目内容
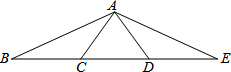 如图,若∠BAC=37°,且AC=BC=AD=DE,则∠BAE=
如图,若∠BAC=37°,且AC=BC=AD=DE,则∠BAE=考点:等腰三角形的性质
专题:
分析:根据等腰三角形的性质和三角形外角的性质可得∠BAC,∠ACD的度数,根据等腰三角形的性质可得∠ADC的度数,根据三角形内角和定理可得∠CAD的度数,根据三角形外角的性质可得∠EAD的度数,继而求得答案.
解答:解:∵∠BAC=37°,且AC=BC=AD=DE,
∴∠BAC=37°,
∴∠ACD=37°+37°=74°,
∴∠ADC=74°,
∴∠CAD=32°,∠EAD=37°,
∴∠BAE=∠BAC+∠CAD+∠EAD=106°.
故答案为:106.
∴∠BAC=37°,
∴∠ACD=37°+37°=74°,
∴∠ADC=74°,
∴∠CAD=32°,∠EAD=37°,
∴∠BAE=∠BAC+∠CAD+∠EAD=106°.
故答案为:106.
点评:考查了等腰三角形的性质,三角形外角的性质,三角形内角和定理的综合运用,关键是得到∠BAC,∠CAD,∠EAD的度数.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
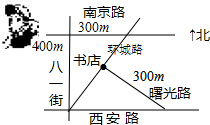 如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )| A、500m | B、525m |
| C、575m | D、625m |