题目内容
顺次连接四边形四边中点所组成的四边形是矩形，则原四边形为（ ）
| A、平行四边形 |
| B、对角线垂直的四边形 |
| C、对角线相等的四边形 |
| D、直角梯形 |
考点：中点四边形
专题：
分析：由于顺次连接四边各边中点得到的四边形是平行四边形，有对应边与原对角线平行，由矩形的性质可知，应为对角线互相垂直的四边形．
解答：解：由矩形的性质知，矩形的四角为直角，即每组邻边互相垂直，故原四边形的对角线应互相垂直．
故选B．
故选B．
点评：本题考查的是矩形的判定定理（有一个角为直角的平行四边形为矩形），难度一般．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
余姚某校为了了解学生在校午餐所需的时间，抽量了20名学生在校午餐所需时间，获得如下的数据（单位：分）：10、12、15、8、16、18、19、18、20、18、18、20、28、22、25、20、15、16、21、16．若将这些数据以4分为组距进行分组，则组数是（ ）
| A、4组 | B、5组 | C、6组 | D、7组 |
下列说法正确的是（ ）
| A、在同一平面内，过已知直线外一点作这条直线的垂线有且只有一条 |
| B、连结直线外一点和直线上任一点，使这条线段垂直于已知直线 |
| C、作出点P到直线的距离 |
| D、连结直线外一点和直线上任一点的线段长是点到直线的距离 |
如图，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个长方形的两边长（x＞y），观察图案及以下关系式：①x-y=n；②xy=| m2-n2 |
| 4 |
| m2-n2 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
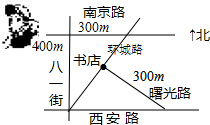如图，西安路与南京路平行，并且与八一街垂直，曙光路与环城路垂直．如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程约为（ ）| A、500m | B、525m |
| C、575m | D、625m |
下列运算正确的是（ ）
| A、（-x-y）2=x2+2xy+y2 |
| B、（-a-b） （a+b）=a2-b2 |
| C、（m-3）（m+2）=m2-6 |
| D、（a-b）2=a2-b2 |