题目内容
15.计算:(1)$\frac{b}{a-b}$+$\frac{{b}^{3}}{{a}^{3}-2{a}^{2}b+a{b}^{2}}$÷$\frac{ab+{b}^{2}}{{b}^{2}-{a}^{2}}$;
(2)$\frac{x+3}{2x-4}$÷($\frac{5}{x-2}$-x-2);
(3)(x+2y-3)(x-2y+3);
(4)[(x+y)2-(x-y)2]÷(2xy);
(5)$\sqrt{1\frac{2}{3}}$÷$\sqrt{2\frac{1}{3}}$×$\sqrt{1\frac{2}{5}}$;
(6)$\frac{2}{b}\sqrt{a{{b}^{5}}}$•(-$\frac{3}{2}\sqrt{{{a}^{3}}b}$)÷3$\sqrt{\frac{b}{a}}$.
分析 (1)原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算,约分即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果;
(3)原式利用平方差公式化简,再利用完全平方公式展开即可得到结果;
(4)原式中括号中利用完全平方公式展开,去括号合并后相除即可得到结果;
(5)原式利用二次根式的乘除法则计算即可得到结果;
(6)原式利用二次根式的乘除法则计算即可得到结果.
解答 解:(1)原式=$\frac{b}{a-b}$+$\frac{{b}^{3}}{a(a-b)^{2}}$•$\frac{-(a+b)(a-b)}{b(a+b)}$=$\frac{b}{a-b}$-$\frac{{b}^{2}}{a(a-b)}$=$\frac{ab-{b}^{2}}{a(a-b)}$=$\frac{b}{a}$;
(2)原式=$\frac{x+3}{2(x-2)}$÷$\frac{5-(x+2)(x-2)}{x-2}$=$\frac{x+3}{2(x-2)}$•$\frac{x-2}{-(x+3)(x-3)}$=-$\frac{1}{2x-6}$;
(3)原式=x2-(2y-3)2=x2-4y2+12y-9;
(4)原式=(x2+2xy+y2-x2+2xy-y2)÷2xy=4xy÷2xy=2;
(5)原式=$\sqrt{\frac{5}{3}×\frac{3}{7}×\frac{7}{5}}$=1;
(6)原式=2b$\sqrt{ab}$•(-$\frac{3}{2}$|a|$\sqrt{ab}$)÷$\frac{3\sqrt{ab}}{|a|}$=-a2b$\sqrt{ab}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

| A. | -5 | B. | 5 | C. | -0.2 | D. | 0.2 |
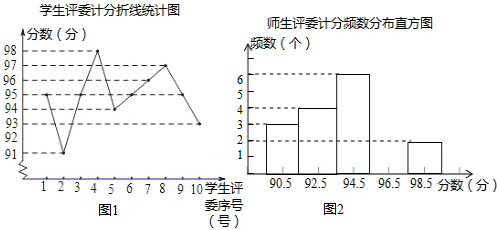
老师评委计分统计表
| 评委序号(号) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 计分(分) | 94 | 96 | 93 | 91 | x | 91 | 91 | 98 | 96 | 93 |
(2)学生评委计分的中位数是95分
(3)计算各班最后得分的规定如下:在评委的计分中各去掉一个最高分、一个最低分,然后计算平均数:分别计算老师、学生评委的平均分:老师、学生评委的平均分各占60%、40%的方法计算各班最后得分,已知七(1)班租后得分为94.4分,求统计表中x的值.
| A. | y1>y2>0 | B. | y1<y2<0 | C. | y2>y1>0 | D. | y2<y1<0 |
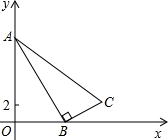 如图,已知Rt△ABC,∠ABC=90°,点A在y轴上,点B在x轴上,AB=10,BC=5,点C(m,3).
如图,已知Rt△ABC,∠ABC=90°,点A在y轴上,点B在x轴上,AB=10,BC=5,点C(m,3).