Question

已知A，B，C是⊙O上的三个点，四边形OABC是平行四边形，那么下列结论中错误的是（　　）

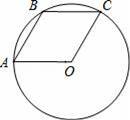
A．∠AOC=120°

B．四边形OABC一定是菱形

C．若连接AC，则AC=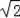OA

D．若连接AC、BO，则AC与BO互相垂直平分

Answer 1

C【考点】圆周角定理；平行四边形的性质；菱形的判定．

【分析】连接OB，AC，根据已知条件得到四边形OABC一定是菱形，根据菱形的性质得到AC与BO互相垂直平分，根据等边三角形的性质得到∠BCO=60°，解直角三角形即可得到结论．

【解答】解：连接OB，AC，

∵四边形OABC是平行四边形，

∵OA=OC，

∴四边形OABC一定是菱形，

∴则AC与BO互相垂直平分，

∵OB=OC，

∴△BCO是等边三角形，

∴∠BCO=60°，

∴∠AOC=120°，

∵∠OAC=30°，

∴AC=OA，

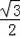
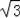
∴AC=OA．

故选C．

【点评】本题考查了圆周角定理，菱形的判定和性质，解直角三角形，熟练掌握菱形的性质是解题的关键．