��Ŀ����
ע�⣺Ϊ��ʹͬѧ�Ǹ��õؽ���⣬�����ṩ��һ�ֽ���˼·��������������˼·�������Ҫ����գ���ɱ���Ľ��Ҳ����ѡ�������Ľ��ⷽ������ʱ������գ�ֻ�谴�ս�����һ��Ҫ����н��
Ҫ��֯һ��������������������ÿ������֮�䶼Ҫ����һ�������ݳ��غ�ʱ������������̼ƻ�����7�죬ÿ�찲��4��������������֯��Ӧ�����ٸ��Ӳ�����
���ⷽ����
�������֯��Ӧ����x���Ӳ�����
��1���ú�x�Ĵ���ʽ��ʾ��
��ôÿ����Ҫ���������������������Ӹ���һ���������ڼӶ��Ҷӵı������ҶӶԼԵı�����ͬһ������������ȫ���ı���һ��������������������
��2���������⣬�г���Ӧ���̣�������������
��3����������̣��ã�������������
��4�����飺��������������
��5������������������
�����㡿һԪ���η��̵�Ӧ�ã�
�����������������֯��Ӧ����x�Ӳ�������ÿ���Ӳμӣ�x��1��������������
 x��x��1���������������г�һ��һԪ���η��̣���⣬��ȥС��0��ֵ�����ɵ�����Ľ����
x��x��1���������������г�һ��һԪ���η��̣���⣬��ȥС��0��ֵ�����ɵ�����Ľ����
����𡿽⣺�������֯��Ӧ����x���Ӳ�����
��1���ú�x�Ĵ���ʽ��ʾ��
��ôÿ����Ҫ��������x��1�����Ӹ���һ���������ڼӶ��Ҷӵı������ҶӶԼԵı�����ͬһ������������ȫ���ı���һ����28����
��2���������⣬�г���Ӧ���̣�
 x��x��1��=28��
x��x��1��=28��
��3����������̣��ã�x1=8��x2=��7��
��4�����飺x2=��7����ȥ����
��5���𣺱�����֯��Ӧ����8�Ӳ�����
�ʴ�Ϊ����x��1����28��
 x��x��1��=28��x1=8��x2=��7��x2=��7����ȥ����������֯��Ӧ����8�Ӳ�����
x��x��1��=28��x1=8��x2=��7��x2=��7����ȥ����������֯��Ӧ����8�Ӳ�����
��������������Ҫ������һԪ���η��̵�Ӧ�ã��������Ĺؼ��ǵõ������ܳ����ĵ�����ϵ��ע��2��֮��ı���ֻ��1���������ܳ���Ӧ����2��


 ����������������������С������nΪ��������
����������������������С������nΪ��������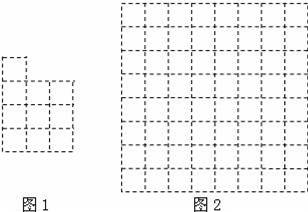


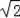
 OA
OA
 ��1��3�IJ�����Ƭ�����dz����ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ������ȡһ�ţ����ÿ�Ƭ�ϵ����ּ�Ϊa����ʹ����x�ķֹ�����
��1��3�IJ�����Ƭ�����dz����ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ������ȡһ�ţ����ÿ�Ƭ�ϵ����ּ�Ϊa����ʹ����x�ķֹ�����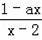
 +2=
+2=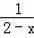
 ��������ĸ�������������������
��������ĸ�������������������