题目内容
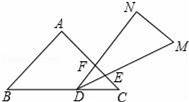
一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E、F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是 .

120° .
【考点】旋转的性质.
【分析】根据等腰三角形的性质和特殊直角三角形的角度求得∠DFC,进一步利用三角形外角的性质即可得到结果.
【解答】解:如图,∵DE=DF,∠EDF=30°,
∴∠DFC=
 (180°﹣∠EDF)=75°,
(180°﹣∠EDF)=75°,
∵∠C=45°,
∴∠BDN=∠DFC+∠C=75°+45°=120°.
故答案为:120°.


【点评】本题考查了旋转的性质,直角三角形的性质,等腰三角形的性质,掌握三角形的内角和与外角的性质是解题的关键.

练习册系列答案
相关题目

 )﹣2﹣(π﹣5)0﹣|﹣3|
)﹣2﹣(π﹣5)0﹣|﹣3|
 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.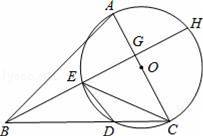

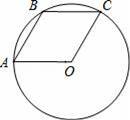

 OA
OA


 B.
B.



 并将不等式组的解集在数轴上表示出来.
并将不等式组的解集在数轴上表示出来.
