题目内容
20.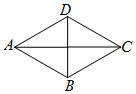 如图,菱形ABCD的边长为5,∠ABC=120°,则此菱形ABCD的面积是( )
如图,菱形ABCD的边长为5,∠ABC=120°,则此菱形ABCD的面积是( )| A. | 20 | B. | 25 | C. | $\frac{25\sqrt{3}}{2}$ | D. | 25$\sqrt{3}$ |
分析 利用菱形的性质求出对角线AC、BD的长即可解决问题.
解答 解:∵四边形ABCD是菱形,∠ABC=120°,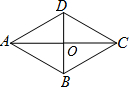
∴∠ABD=∠CBD=60°,AC⊥BD,
∴∠AOB=90°,
∵AB=5,
在Rt△AOB中,OB=$\frac{1}{2}$AB=$\frac{5}{2}$,
∴OA=$\sqrt{3}$OB=$\frac{5\sqrt{3}}{2}$,
∴BD=5,AC=5$\sqrt{3}$,
∴S菱形ABCD=$\frac{1}{2}$•AC•BD=$\frac{1}{2}$•5•5$\sqrt{3}$=$\frac{25\sqrt{3}}{2}$,
故选C.
点评 本题主要考查的是菱形的性质,等边三角形的性质和判定,含30度角的直角三角形性质,三角形的面积等知识点的应用,注意:菱形性质有菱形的四条边都相等、对角线互相垂直平分、每条对角线平分一组对角.菱形的面积等于对角线乘积的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.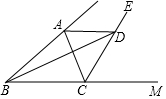 如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )
如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )
 如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )
如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )| A. | m-a>b-n | B. | m-a<b-n | ||
| C. | m-a=b-n | D. | m-a>b-n或m-a<b-n |
8.交换下列命题的题设和结论,得到的新命题是假命题的是( )
| A. | 两直线平行,同位角相等 | B. | 相等的角是对顶角 | ||
| C. | 所有的直角都是相等的 | D. | 若a=b,则a-3=b-3 |
15.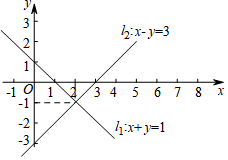 如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )
如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )
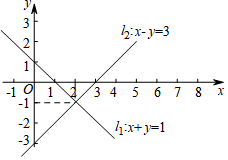 如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )
如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ |