题目内容
在平面直角坐标系xOy中,已知抛物线C1:y=-mx2+2mx+4(m≠0)与抛物线C2:y=x2-2x,
(1)抛物线C1与y轴交于点A,其对称轴与x轴交于点B.求点A,B的坐标;
(2)若抛物线C1在-2<x<-1这一段位于C2下方,并且抛物线C1在1<x<3这一段位于C2上方,求抛物线C1的解析式.
(1)抛物线C1与y轴交于点A,其对称轴与x轴交于点B.求点A,B的坐标;
(2)若抛物线C1在-2<x<-1这一段位于C2下方,并且抛物线C1在1<x<3这一段位于C2上方,求抛物线C1的解析式.
考点:二次函数的性质,待定系数法求二次函数解析式
专题:计算题
分析:(1)对于y=-mx2+2mx+4,求自变量为0时的函数值即可得到A点坐标;根据二次函数的性质求出抛物线C1的对称轴即可得到B点坐标;
(2)先求抛物线C2:y=x2-2x的对称轴得到抛物线C1和抛物线C2的对称轴都是直线x=1,根据抛物线的对称性,当抛物线C1在-2<x<-1这一段位于C2下方,则抛物线C1在3<x<4这一段位于C2下方,加上抛物线C1在1<x<3这一段位于C2上方,于是得到两条抛物线的交点横坐标为x=3,利用y=x2-2x可确定交点坐标,然后把交点坐标代入y=-mx2+2mx+4中求出m即可.
(2)先求抛物线C2:y=x2-2x的对称轴得到抛物线C1和抛物线C2的对称轴都是直线x=1,根据抛物线的对称性,当抛物线C1在-2<x<-1这一段位于C2下方,则抛物线C1在3<x<4这一段位于C2下方,加上抛物线C1在1<x<3这一段位于C2上方,于是得到两条抛物线的交点横坐标为x=3,利用y=x2-2x可确定交点坐标,然后把交点坐标代入y=-mx2+2mx+4中求出m即可.
解答:解:(1)当x=0时,y=-mx2+2mx+4=4,则A点坐标为(0,4),
抛物线的对称轴为直线x=-
=1,则B点坐标为(1,0);
(2)抛物线C2:y=x2-2x的对称轴为直线x=-
=1,
则抛物线C1和抛物线C2的对称轴都是直线x=1,
由于抛物线C1在-2<x<-1这一段位于C2下方,则抛物线C1在3<x<4这一段位于C2下方,
而抛物线C1在1<x<3这一段位于C2上方,
所以两条抛物线的交点横坐标为x=3,
当x=3时,y=x2-2x9-2×3=3,即两抛物线的交点坐标为(3,3),
把(3,3)代入y=-mx2+2mx+4得-9m+6m+4=3,解得m=
,
所以抛物线C1的解析式y=-
x2+
x+4.
抛物线的对称轴为直线x=-
| 2m |
| 2×(-m) |
(2)抛物线C2:y=x2-2x的对称轴为直线x=-
| -2 |
| 2×1 |
则抛物线C1和抛物线C2的对称轴都是直线x=1,
由于抛物线C1在-2<x<-1这一段位于C2下方,则抛物线C1在3<x<4这一段位于C2下方,
而抛物线C1在1<x<3这一段位于C2上方,
所以两条抛物线的交点横坐标为x=3,
当x=3时,y=x2-2x9-2×3=3,即两抛物线的交点坐标为(3,3),
把(3,3)代入y=-mx2+2mx+4得-9m+6m+4=3,解得m=
| 1 |
| 3 |
所以抛物线C1的解析式y=-
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
下列说法中正确的是( )
| A、不确定事件发生的概率是不确定的 |
| B、事件发生的概率可以等于事件不发生的概率 |
| C、事件发生的概率不可能等于0 |
| D、抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于2 |
 如图,点A,B,C均在⊙O上,∠ACB=35°,则∠AOB的度数为( )
如图,点A,B,C均在⊙O上,∠ACB=35°,则∠AOB的度数为( )| A、20° | B、40° |
| C、60° | D、70° |
 有理数a,b,c在数轴上的位置如图所示,则|c+a|-|b-a+c|=
有理数a,b,c在数轴上的位置如图所示,则|c+a|-|b-a+c|= 如图,△ABC中,AB=AC,D是BC中点,BE⊥AC于E,求证:△ACD∽△BCE.
如图,△ABC中,AB=AC,D是BC中点,BE⊥AC于E,求证:△ACD∽△BCE.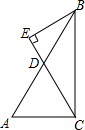 如图,△ABC中,∠ACB=90°,sinA=
如图,△ABC中,∠ACB=90°,sinA=